Сжатие и его частные виды

Найдём собственные числа λ преобразования сжатия (24) из условия 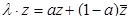. Составим систему из этого условия и сопряжённого к нему выражения: 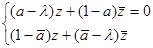. Чтобы найти собственные числа, нужно решить уравнение 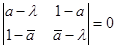, откуда получим  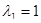и .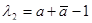

Примем без доказательства следующую теорему [1]: если λ – собственное действительное число аффинного преобразования, то множество точек, каждая из которых делит в отношении 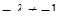 отрезок, соединяющий точку с её прообразом, есть двойная прямая этого преобразования.

Очевидно, что прямые MM’  и NN’ (рис.18) являются двойными прямыми и λ₂ – действительное число, то точка Р делит отрезок MM’ в отношении 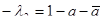, то есть 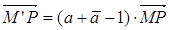. Число 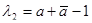= δ называется коэффициентом сжатия. Если а – действительное число, то направление сжатия перпендикулярно его оси и сжатие называется прямым (ортогональным) сжатием.

Рассмотрим частный случай сжатия – косую симметрию [1]. Это инволютивное преобразование, то есть оно тождественно преобразованию, обратному ему. Преобразование, обратное (24), имеет формулу:

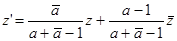                                                   (25)

Оно имеет ту же ось, что и (24). Равенство преобразований (24) и (25) имеет место тогда и только тогда, когда 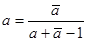, откуда , то есть а – чисто мнимое число. Таким образом, формулой (24) при условии 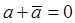 задаётся косая симметрия с действительной осью. В этом случае коэффициент сжатия равен 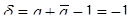, следовательно, ось косой симметрии делит пополам каждый отрезок, соединяющий соответственные точки. Косая симметрия – аффинное преобразование второго рода, так как его определитель отрицателен.

Если а=0, получаем осевую симметрию относительно действительной оси. Осевая симметрия – аффинное преобразование также второго рода ().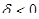

Список литературы:

1. Скопец З.А. Геометрические миниатюры / Сост. Г.Д. Глейзер. – М.: Просвещение, 1990

2.  Яглом И.М., Ашкинузе В.Г. Идеи и методы аффинной и проективной геометрии. Часть 1. Аффинная геометрия. М.: - Учпедгиз, 1962

3.  Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. - 6-е изд., перераб. - М.: Наука, 1988.

4.  Умное А.Е. Аналитическая геометрия и линейная алгебра. - Долгопрудный: ЗАО Оптимизационные системы и технологии, 1997.

5. Кострикин А.И. Введение в алгебру. -М.: Наука, 1975.

6. Мальцев А.И. Основы линейной алгебры. - 4-е изд. -М.: Наука, 1976.

7. Постников М.М. Лекции по геометрии. Семестр 2. -М.: Наука, 1979.

8. Чехлов В. И. Лекции по аналитической геометрии и линейной алгебре. - М.: МФТИ, 2000.

9. Шарипов Р. А. Курс линейной алгебры и многомерной геометрии: учебное пособие для вузов / Издание Башкирского ун-та. ≈ Уфа, 1996. ≈ 226 с. ≈ ISBN 5-7477-0099-5

10. Бахвалов С.В., Моденов П.С., Пархоменко А.С. Сборник задач по аналитической геометрии. — М.: Наука, 1964.

11. Ильин В. А., Поэняк Э. Г. Аналитическая геометрия. — М.: Наука, 1981.

12. Цубербиллер О. Н. Задачи и упражнения по аналитической геометрии. — М.: Наука, 1970.