Экстремум функции двух независимых переменных

Функция u = f (x, y) имеет максимум (минимум) в точке M (x ₀, y ₀), если значение функции в этой точке больше (меньше), чем ее значение в любой другой точке M (x, y) некоторой окрестности точки , т.е. f (x ₀, y ₀) > f (x, y) или f (x ₀, y ₀) < f (x, y) для всех точек M (x, y), отличных от точки  и удовлетворяющих условию , где d — некоторое положительное число.

Максимум или минимум функции называется ее экстремумом. Точка , в которой функция имеет экстремум, называется точкой экстремума.

Необходимые условия экстремума

Если дифференцируемая функция u = f (x, y) достигает экстремума
в точке M (x ₀, y ₀), то ее частные производные первого порядка в этой точке равны нулю, т.е. , .Точки, в которых частные производные равны нулю, называются стационарными точками. Не всякая стационарная точка является точкой экстремума.

Достаточные условия экстремума

Пусть  — стационарная точка функции 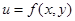. Обозначим

                , ,

                         и составим дискриминант .

Тогда, если , то функция имеет в точке  экстремум, а именно максимум при  (или ) и минимум при  (или );

если , то в этой точке  экстремума нет;

если , то требуется дальнейшее исследование.

Пример. Исследовать функцию на экстремум

 .

Решение: найдем частные производные первого порядка:

 ;  .

Приравняем нулю эти выражения и решим получившуюся систему относительно и . В результате:      

Решая систему, найдем координаты точки, подозрительной на экстремум. Такой точкой является точка . Экстремума в этой точке может и не быть.

Наличие экстремума в подозрительных точках устанавливается с помощью производных второго порядка.

Так как , экстремум есть.

Поскольку обе величины  и , в точке  функция  имеет максимум. Вычислим значение функции в найденной точке:

 .

Таким образом, данная функция имеет один экстремум в точке . Это максимум, и его значение равно .