2020-05-21
137
а) Если дуга гладкой кривой 
вращается вокруг оси Ох, то площадь поверхности вращения вычисляется по формуле:
б) Если кривая задана параметрическими уравнениями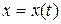 
и 
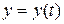, то
Контрольные вопросы
1. Основные свойства определенного интеграла.
2. Формулы для вычисления площадей криволинейных трапеций, ограниченных кривыми и отрезками.
Раздел 5. Численные методы решения прикладных задач
Тема5.1.Приближенное решений уравнений. Интерполирование.
Метод хорд. Метод Касательных. Метод итераций. Интерполяционный многочлен Лагранжа.
Цели занятия:
Должен уметь: находить приближенные решения уравнений; интерполяционный многочлен Лагранжа.
Должен знать: Метод хорд. Метод Касательных. Метод итераций. Интерполяционный многочлен Лагранжа.
Приближенное решение нелинейных уравнений
Нелинейными уравнениями называются уравнения вида 
.
Здесь 
– нелинейная функция:
– нелинейная алгебраическая функция вида 
;
– трансцендентные функции – тригонометрические, обратные тригонометрические, логарифмические, показательные и гиперболические функции;
– комбинирование этих функций 
.
Задача о нахождении приближенных значений действительных корней уравнения 
предусматривает предварительное отделение корня, т.е. установление промежутка, в котором других корней данного уравнения нет. Будем предполагать, что функция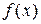 
в промежутке 
непрерывна вместе со своими производными 
и 
, значения 
и 
функции на концах промежутка имеют разные знаки, т.е. 
и обе производные сохраняют знак во всем промежутке.
Метод хорд
Пусть требуется вычислить действительный корень уравнения , изолированный на отрезке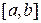 
. Рассмотрим график функции 
. Пусть 
и 
. Точки графика 
и 
соединим хордой. За приближенное значение искомого корня примем абсциссу x 1 точки пересечения хорды AB с осью Ох.
Это приближенное значение находится по формуле
,
где 
. Пусть, например, 
, тогда за новый (более узкий) промежуток изоляции корня можно принять 
. Соединив точки 
и , получим в точке пересечения хорды с осью Ох второе приближение x 2, которое вычислим по формуле
,
и т.д. Последовательность чисел 
стремится к искомому корню уравнения 
. Вычисление приближенных значений корней уравнения следует вести до тех пор, пока не перестанут изменяться те десятичные знаки, которые мы хотим сохранить в ответе (т.е. пока не будет достигнута заданная степень точности).
Метод итераций
Пусть известно, что нелинейное уравнение 
имеет на отрезке единственный вещественный корень 
. Требуется найти этот корень с заданной точностью. Применяя тождественные преобразования, приведем уравнение к виду
Выберем произвольно приближенное значение корня 
и вычислим 
. Найденное значение 
подставим в правую часть соотношения и вычислим 
. Продолжая процесс вычислений дальше, получим числовую последовательность 
. Если существует предел этой последовательности, то он и является корнем уравнения. В самом деле, пусть 
. Тогда, переходя к пределу в равенстве 
и учитывая непрерывность функции 
на отрезке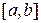 
, получим 
или 
.
Корень можно вычислить с заданной точностью ε по итерационной формуле
Достаточное условие, при котором итерационный процесс сходится, определяет следующая
Теорема: Пусть функция 
определена и дифференцируема на отрезке 
, причем все ее значения 
и выполняется условие
,
тогда процесс итераций (7) сходится независимо от начального значения 
и предельное значение 
является единственным корнем уравнения (6) на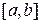 
. Точка 
называется неподвижной точкой для уравнения.
Итерационный процесс поиска корня прекращается, как только выполнится условие 
.
