Б) разложение произвольного вектора АВ по базису

(х₂ – х₁)i+(у₂ – у₁)j+(z₂ – z₁)k.

Правило 2. Для разложения вектора по базису нужно каждую координату вектора умножить на соответствующий координатный (базисный) вектор.

5. Действия с векторами в координатной форме:

Правило 3. Суммой (разностью) векторов 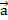 (х₁; у₁; z₁) и  (х₂; у₂; z₂) называется вектор  = , координаты которого равны сумме (разности) соответствующих координат этих векторов:

 (х₁  х₂; у₁  у₂; z₁  z₂).

Правило 4. Произведением вектора  (х; у; z) на число k называется вектор

=k 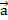, координаты которого равны произведению числа k на координаты вектора :

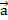 =(kх; kу; kz).

Правило 5. Построение точки в пространстве

Для построения точки в пространстве необходимо:

1) Построить прямоугольную систему координат в пространстве Охуz.

2) Отложить первые две координаты на соответствующих осях и провести их проекции;

3) Выполнить параллельный перенос третьей координаты в точку пересечения проекций;

Правило 6. Построение радиус-вектора в пространстве

Для построения радиус-вектора в пространстве необходимо:

1) Построить прямоугольную систему координат в пространстве Охуz.

2) Отложить первые две координаты конца вектора на соответствующих осях и провести их проекции;

3) Выполнить параллельный перенос третьей координаты в точку пересечения проекций;

4) Соединить полученную точку с началом координат и обозначить искомый вектор.

 

   Правило 7. Построение вектора MN в пространстве

Для построения вектора MN в пространстве необходимо:

1) Построить прямоугольную систему координат в пространстве Охуz.

2) По правилу (5) построить 2 точки - точку начала вектора M(-2;0;3) и точку конца N(2;1; -2).

3) Соединить полученные точки и обозначить искомый вектор.

 

     

 

Рассмотрим правила, которые позволяют по координатам данных векторов найти координаты их суммы и разности, а также координаты произведения данного вектора на данное число.

 

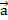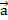1°. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Другими словами, если  {х₁; у₁; z₁} и {х₂; у₂; z ₂} — данные векторы, то вектор  +  имеет координаты {х₁ + х₂; у₁ + у₂; z₁ + z₂}.

 

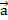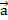2°. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Другими словами, если  {х₁; у₁; z₁} и {х₂; у₂; z ₂}- данные векторы, то вектор  -  имеет координаты {х₁ - х₂; у₁ - у₂; z₁ - z₂}.

 

3°. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. Другими словами, если 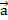 {х; у; z }— данный вектор, α — данное число, то вектор α 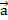имеет координаты { α х; α у; α z }.

 

Утверждения 1°—3° доказываются точно так же, как и для векторов на плоскости.

Рассмотренные правила позволяют находить координаты любого вектора, представленного в виде алгебраической суммы данных векторов, координаты которых известны. Рассмотрим пример. Задача

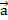Найти координаты вектора  = 2 -  + , если 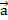 {1; -2; 0},  {0; 3; -6}, {-2; 3; 1}.

Решение

По правилу 3° вектор 2 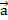 имеет координаты {2; -4; 0}, а вектор - — координаты {0; -1; 2}.

Так как  = 2 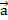-  + , то его координаты {х; у; z} можно вычислить по правилу 1°:

х = 2 + 0 - 2 = 0, у = -4 -1 + 3 = -2, z = 0 + 2 + 1 = 3. Итак, вектор  имеет координаты {0; -2; 3}.