Інтервальне оцінювання параметрів

Інтервальною називають оцінку, що визначається двома числами – кінцями інтервалу. Інтервальні оцінки дозволяють визначити точність і надійність точкових оцінок.

Надійністю (довірчою ймовірністю) оцінки невідомого параметра за допомогою знайденої за даними вибірки статистичної характеристики називають ймовірність , з якою виконується нерівність :

чи, що те ж саме

Звичайно використовують рівень надійності, що має значення: 0,95; 0,99 і 0,999.

Довірчим називають інтервал ( ), який покриває невідомий параметр із заданою надійністю .

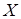1 Довірчі інтервали для оцінки математичного сподівання нормального розподілу при відомому . Розглянемо задачу інтервальної оцінки невідомого математичного сподівання кількісної ознаки по вибірковій
середній нормально розподіленої сукупності з відомим середньо квадратичним відхиленням . Знайдемо довірчий інтервал, що покриває параметр з надійністю .

Вибіркова середня змінюється від вибірки до вибірки. Тому її можна розглядати, як випадкову величину , а вибіркові значення ознаки , ,..., (ці числа також змінюються від вибірки до вибірки) – як однаково розподілені незалежні випадкові величини , ,..., . Тобто, математичне сподівання кожної з цих величин дорівнює і середнє квадратичне відхилення – .

Можна показати, що у разі нормального розподілення випадкової величина вибіркова середня , знайдена за незалежними спостереженнями, також розподілена нормально з параметрами:

, . (12)

Поставимо вимогу, щоб було виконано співвідношення

, (13)

де – задана надійність.

Застосуємо до нормально розподіленої випадкової величини відому з теорії ймовірностей формулу про ймовірність відхилення нормально розподіленої випадкової величини зі середньоквадратичним відхиленням від його математичного сподівання не більше ніж на

, (14)

де – табульована функція Лапласа (3).

При цьому у формулі (14) відповідно до (12) необхідно замінити на , на , залишивши математичне чекання без зміни.

Тоді одержимо:

, (15)

де введено таке позначення

. (16)

Підставивши у формулу (15) вираз величини через з (16)

, (17)

перетворивши її до вигляду:

З огляду на те, що ймовірність задана і дорівнює (13), а також, що випадкова величина є формальним поданням вибіркової середньої , остаточно одержимо:

. (18)

Цю оцінку називають класичною. Відповідно до неї з надійністю можна стверджувати, що довірчий інтервал покриває невідомий параметр . При цьому величина визначається з рівності (18), а точність оцінки – з (17).

З формули (17) видно, що із зростанням обсягу вибірки величина зменшується, тобто точність оцінки підвищується. З співвідношення (18), де , із врахуванням відомого зростаючого характеру функції Лапласа (3), випливає, що підвищення надійності класичної оцінки (18) призводить до погіршення її точності.

2 Довірчі інтервали для оцінки математичного сподівання нормального розподілу при невідомому . Ускладнимо постановку задачі, розглянутої в попередньому пункті, вважаючи, що тепер середнє квадратичне відхилення нормально розподіленої кількісної ознаки невідомо.

У цьому випадку за даними вибірки побудуємо випадкову величину (її значення будемо традиційно позначати відповідною малою буквою ), що є функціональним перетворенням випадкової величини , введеної в попередньому пункті:

. (19)

Тут збережено позначення, які введені в попередньому пункті. Крім того, вжито , що є "виправлене" середнє квадратичне відхилення (1.7).

Можна показати, що випадкова величина (19) має розподіл Стьюдента (2.8) з ступенями волі і щільністю розподілу:

Де

– Гама-функція Эйлера (2.4).

Очевидно, що розподіл Стьюдента визначається параметром – обсягом вибірки та не залежить від невідомих параметрів і , що зумовило його практичну цінність. Оскільки функція є парною відносно , ймовірність виконання нерівності можна перетворити таким чином:

При заміні нерівності в круглих дужках на еквівалентну йому подвійну нерівність і заміні на так само, як у попередньому пункті, остаточно одержимо:

Тобто, використовуючи розподіл Стьюдента, можна знайти довірчий інтервал , що покриває невідомий параметр із надійністю . Величина при цьому знаходиться в таблиці розподілу Стьюдента у залежності від значень параметрів і .

3 Довірчі інтервали для оцінки середнього квадратичного відхилення нормального розподілу. Тепер вирішимо задачу інтервальної оцінки з надійністю невідомого генерального середнього квадратичного відхилення нормально розподіленої кількісної ознаки за його "виправленим" вибірковим середньо квадратичним відхиленням s. Це означає, що має виконуватися умова:

чи, що те ж саме,

. (20)

Подвійну нерівність у виразі (20) зручно перетворити до вигляду:

(21)

, (22)

де введено позначення

(23)

і враховано, що відхилення відносно , тобто – мала величина в порівнянні з , так що .

Вибіркове середнє квадратичне відхилення змінюється від вибірки до вибірки, тому його можна розглядати як випадкову величину, що ми дотримуючись традиції позначимо відповідною великою літерою . Помноживши всі члени останньої нерівності (22) на , одержимо нову нерівність

що після введення позначення

(24)

прийме остаточний вигляд:

. (25)

Відзначимо, що нерівності (21) і (25) еквівалентні. Тому рівність (20) можна тепер переписати так:

. (26)

Пірсон показав, що величина (24) після її підвищення до квадрату, тобто у вигляді , підкоряється закону розподілу "хі-квадрат" (5), тому і має таке позначення. Можна показати, що щільність розподілу самої випадкової величини має при цьому наступний вигляд:

. (27)

Важлива особливість цього розподілу полягає в тому, що воно є інваріантним відносно оцінюваного параметра , і залежить лише від обсягу вибірки .

Відомо, що ймовірність неперервній випадковій величині знаходитися на інтервалі ( , ) виражається у такий спосіб через щільність її розподілу:

Застосувавши цю формулу в нашому конкретному випадку ймовірності перебування випадкової величини (24) із щільністю у вигляді (27) на інтервалі (25), одержимо:

. (28)

Співвідношення (28) можна розглядати як рівняння щодо невідомої величини (23) при заданих значеннях і . Це рівняння було розв’язано в загальному вигляді зі складанням таблиць, по яких можна знайти значення . Знаючи величину і "виправлене" вибіркове середнє квадратичне відхилення s по формулам (21), (23) визначаємо довірчий інтервал для оцінки середнього квадратичного відхилення нормального розподілу.

4 Оцінки істинного значення величини, що вимірюється, і точності вимірів. Ця задача подає великий практичний інтерес для метрології.

Нехай проведено незалежних однаково точних вимірів деякої фізичної величини, істинне значення якої невідомо. До того ж невідомо також і середнє квадратичне відхилення випадкових похибок вимірювання. Результати окремих вимірів , ,..., можна розглядати, як випадкові величини , ,..., , що є незалежні (виміри незалежні), мають те ж саме математичне сподівання (істинне значення величини, що вимірюється), однакові дисперсії (виміри однаково точні) і нормально розподілені (таке допущення підтверджується досвідом).

Отже, усі припущення, що було зроблено під час отримання довірчих інтервалів у пунктах 1 і 2, виконуються. Тому можна безпосередньо використати отримані в них формули. Іншими словами, істинне значення величини, що вимірюється, можна оцінювати по середньому арифметичному результатів окремих вимірів за допомогою довірчих інтервалів.

Середнє квадратичне відхилення випадкових похибок вимірів у теорії помилок характеризує точність вимірів (точність приладу).

Для оцінки використовують "виправлене" середнє квадратичне відхилення . Оскільки звичайно результати вимірів взаємно незалежні, мають одне й теж саме математичне сподівання (істинне значення величини, що вимірюється) і однакову дисперсію (у випадку однаково точних вимірів), то теорію, викладену в пункті 3, можна застосувати і для оцінки точності вимірів.

5 Інтервальна оцінка ймовірності біноміального розподілу. У підрозділі 2 у якості приклада 1 було вирішено задачу точкової оцінки ймовірності біноміального розподілу. Як точкову оцінку невідомої ймовірності було узято відносну частоту появи події ( – число появ події, – число випробувань). Було отримано математичне сподівання і дисперсію оцінки.

Тепер буде знайдено довірчий інтервал для оцінки ймовірності за відносною частотою.

Для спрощення припустимо, що кількість іспитів досить велика, а ймовірність не є близькою ні до одиниці, ні до нуля (досить, щоб обидві величини і були більше чотирьох). Тоді можна вважати, що частота події є випадковою величиною , розподіл якої є наближеним до нормального закону (у сенсі функції розподілу). Параметрами цього закону будуть і .

Тому до випадкової величини можна застосувати відому формулу про ймовірність відхилення нормально розподіленої випадкової величини зі середньо квадратичним відхиленням від її математичного сподівання не більше ніж на

, (29)

де – табульована функція Лапласа.

Зажадавши, щоб умова для ймовірності у формулі (29) виконувалося з надійністю , і, замінивши в ній на , на , на , а також увівши позначення , одержимо

або інакше

При практичному застосуванні цієї формули випадкову величину необхідно замінити невипадковою відносною частотою , що спостерігається, і підставити :

Під час розв’язання цієї нерівності щодо невідомої ймовірності у припущенні підвищимо до квадрата обидві її частини. При цьому одержимо еквівалентну квадратну нерівність відносно :

Її коефіцієнт при старшому члені та дискримінант позитивні, тому її корені і дійсні, причому не дорівнюють один одному. Отже ця нерівність має розв’язання: