Задание 1. Вычислить указанные определённые интегралы.
Вариант 0.
1. 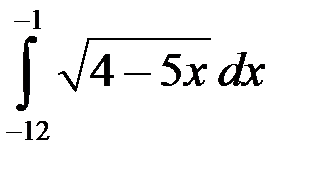 ; 2.
; 2. 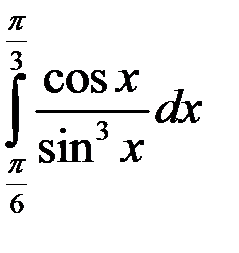 ; 3.
; 3. 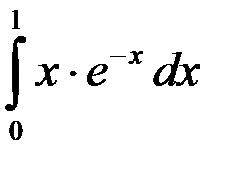 ; 4.
; 4. 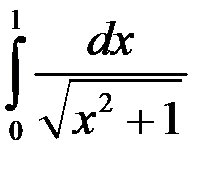 .
.
Вариант 1.
1. 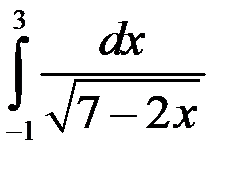 ; 2.
; 2. 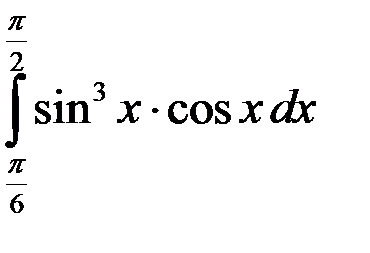 ; 3.
; 3. 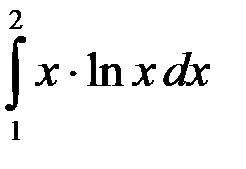 ; 4.
; 4. 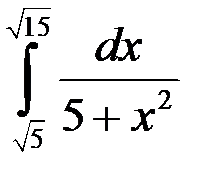 .
.
Вариант 2.
1. 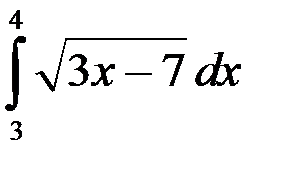 ; 2.
; 2. 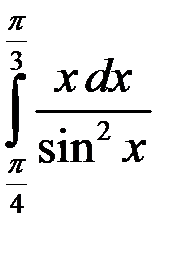 ; 3.
; 3. 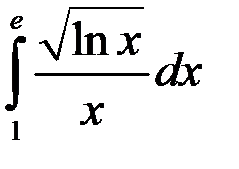 ; 4.
; 4. 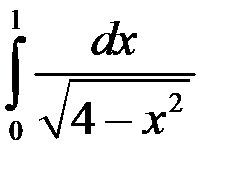 .
.
Вариант 3.
1. 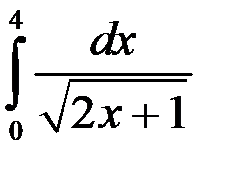 ; 2.
; 2. 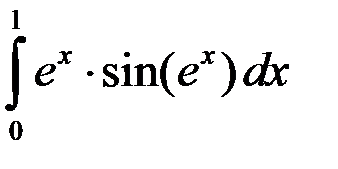 ; 3.
; 3. 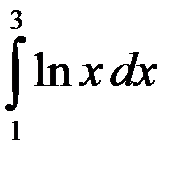 ; 4.
; 4. 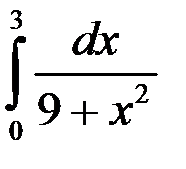 .
.
Вариант 4.
1. 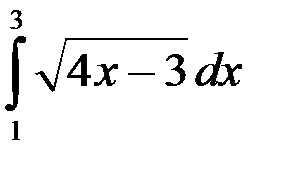 ; 2.
; 2. 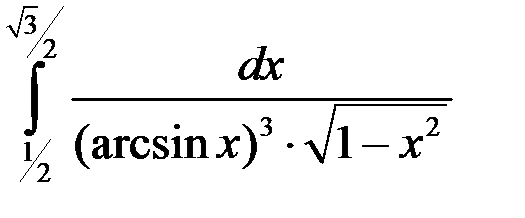 ; 3.
; 3. 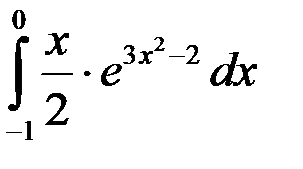 ; 4.
; 4. 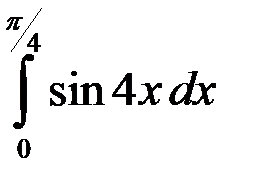 .
.
Вариант 5.
1. 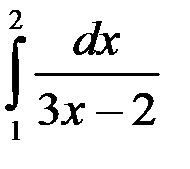 ; 2.
; 2. 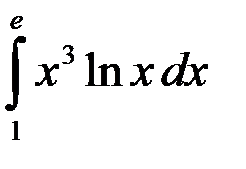 ; 3.
; 3. 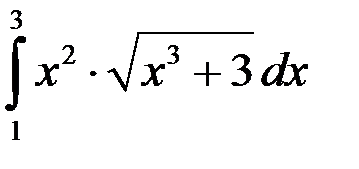 ; 4.
; 4. 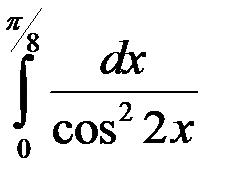 .
.
Вариант 6.
1. 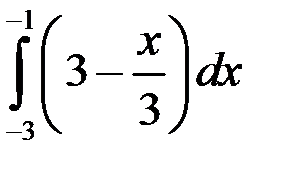 ; 2.
; 2. 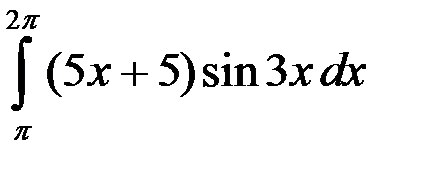 ; 3.
; 3. 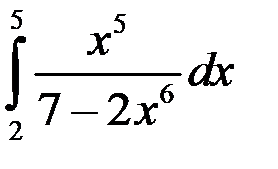 ; 4.
; 4. 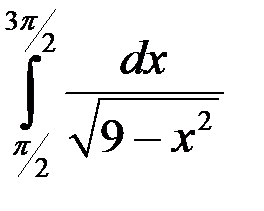 .
.
Вариант 7.
1. 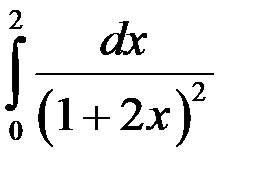 ; 2.
; 2. 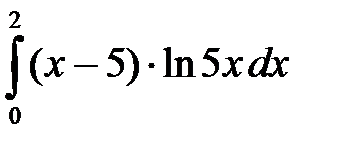 ; 3.
; 3. 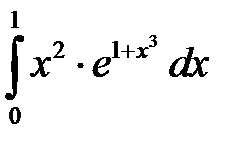 ; 4.
; 4. 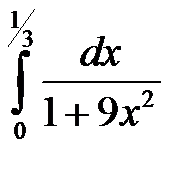 .
.
Вариант 8.
1. 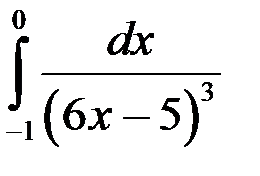 ; 2.
; 2. 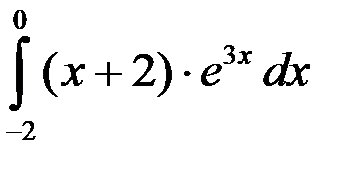 ; 3.
; 3. 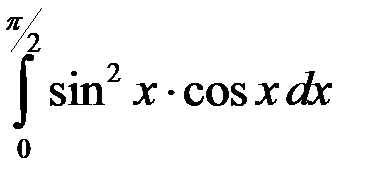 ; 4.
; 4. 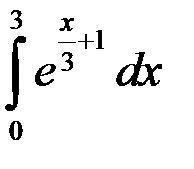 .
.
Вариант 9.
1. 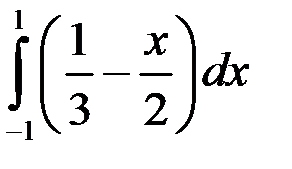 ; 2.
; 2. 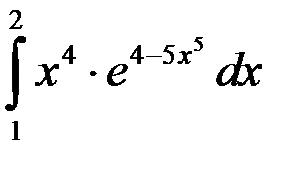 ; 3.
; 3. 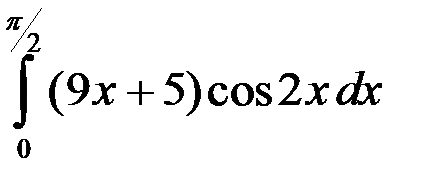 ; 4.
; 4. 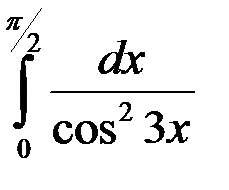 .
.
Задание 2. Построить фигуру, ограниченную заданными линиями, и вычислить её площадь.
Вариант 0. 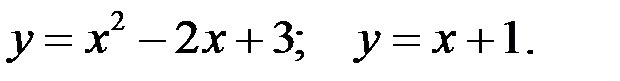
Вариант 1. 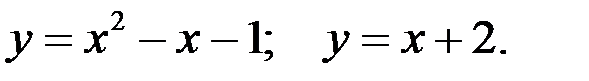
Вариант 2. 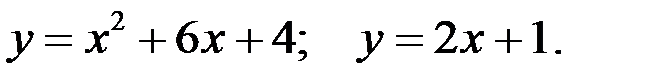
Вариант 3. 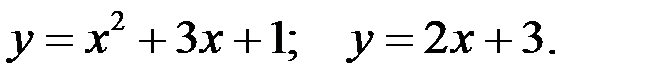
Вариант 4. 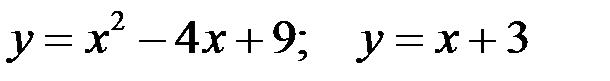 .
.
Вариант 5. 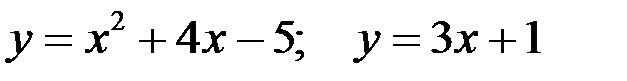 .
.
Вариант 6. 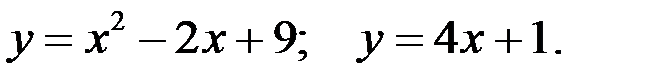
Вариант 7. 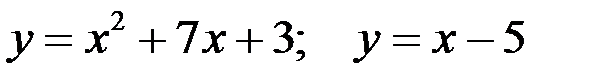 .
.
Вариант 8. 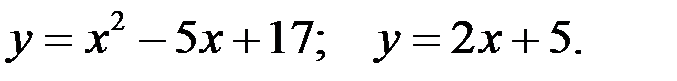
Вариант 9. 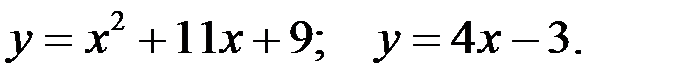
Задание 3. Вычислить объём тела, получающегося при вращении вокруг оси 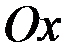 фигуры, ограниченной линиями, уравнения которых заданы.
фигуры, ограниченной линиями, уравнения которых заданы.
Вариант 0. 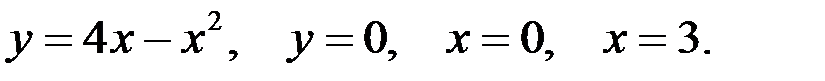
Вариант 1. 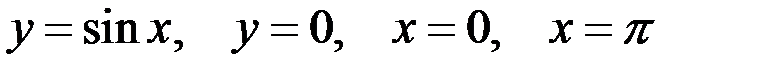 .
.
Вариант 2. 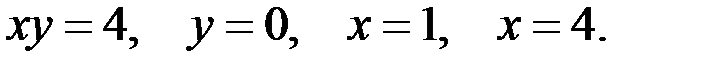
Вариант 3. 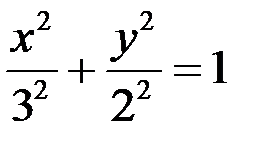 .
.
Вариант 4. 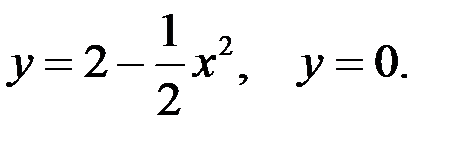
Вариант 5. 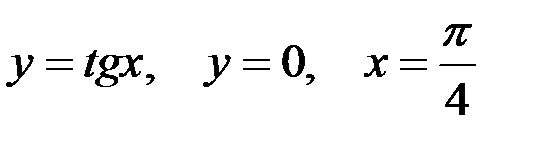 .
.
Вариант 6. 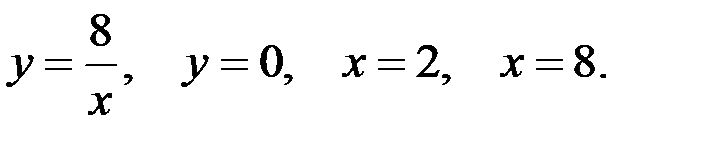
Вариант 7. 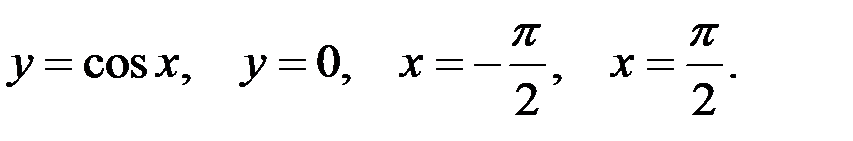
Вариант 8. 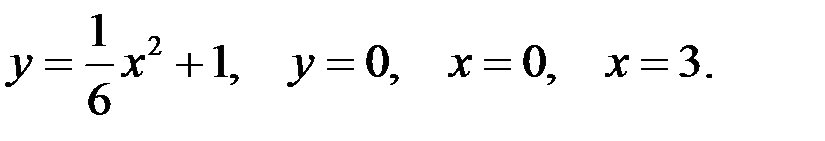
Вариант 9. 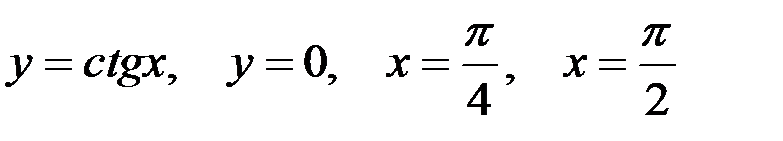 .
.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Практическая часть
Пример 1. Найти решение задачи Коши для ДУ первого порядка
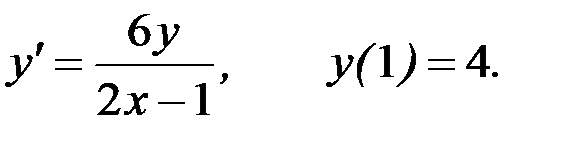
Решение. Данное уравнение является дифференциальным уравнением с разделяющимися переменными, то есть уравнением вида 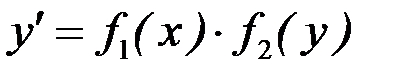 (здесь
(здесь 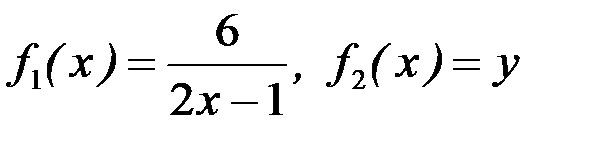 ). Запишем его в виде
). Запишем его в виде 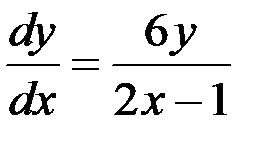 . Разделив обе части уравнения на
. Разделив обе части уравнения на 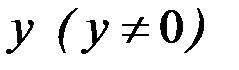 и умножив на
и умножив на 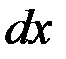 , получаем ДУ с разделенными переменными
, получаем ДУ с разделенными переменными
|
|
|
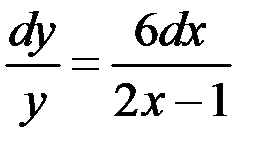 ,
,
в левой части которого отсутствуют члены, содержащие 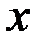 , и в правой части которого отсутствуют члены, содержащие
, и в правой части которого отсутствуют члены, содержащие 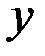 . Интегрируя обе части последнего уравнения, получаем
. Интегрируя обе части последнего уравнения, получаем 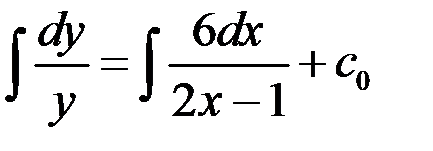 ,
,
или 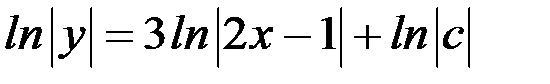
(здесь символ 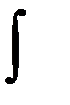 обозначает какую-либо одну первообразную, произвольная постоянная
обозначает какую-либо одну первообразную, произвольная постоянная 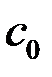 взята в логарифмическом виде для удобства). После потенцирования получаем общее решение исходного ДУ
взята в логарифмическом виде для удобства). После потенцирования получаем общее решение исходного ДУ
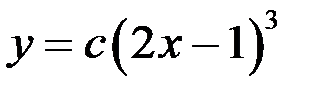 .
.
Заметим, что здесь постоянная 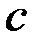 может принимать любое действительное значение, в частности значение
может принимать любое действительное значение, в частности значение 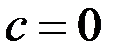 , так как при
, так как при 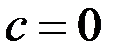 получаем функцию
получаем функцию 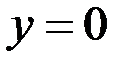 , которая также является решением исходного уравнения.
, которая также является решением исходного уравнения.
Для того чтобы выделить из общего решения решение, удовлетворяющее условию 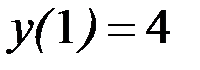 , определим значение постоянной
, определим значение постоянной 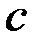 так, чтобы это условие оказалось выполненным.
так, чтобы это условие оказалось выполненным.
Подставив в общее решение 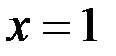 и
и 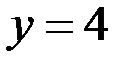 , получаем
, получаем 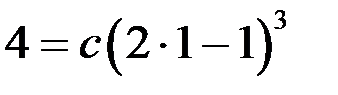 , отсюда
, отсюда 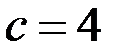 . Следовательно,
. Следовательно,
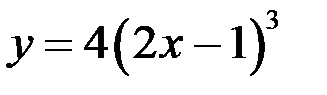 – искомое решение задачи Коши.
– искомое решение задачи Коши.
Пример 2. Найти общее решение дифференциального уравнения
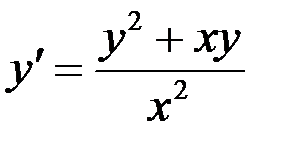 .
.
Решение. Запишем уравнение в виде
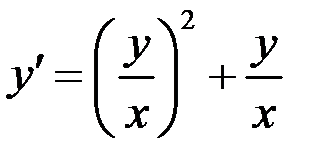 .
.
Данное уравнение является однородным ДУ первого порядка, то есть уравнением вида 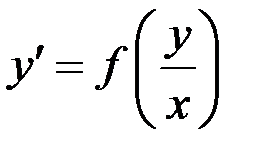 (здесь
(здесь 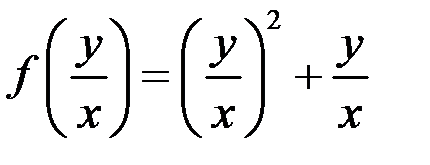 ). Для его решения сделаем подстановку
). Для его решения сделаем подстановку 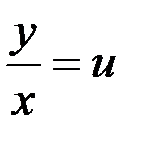 . Отсюда
. Отсюда 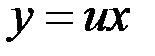 и
и 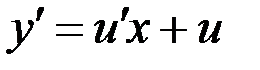 . Подставляя выражения для
. Подставляя выражения для 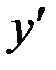 и
и 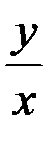 в последнее ДУ, получаем
в последнее ДУ, получаем
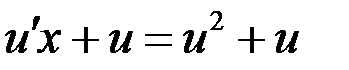 ,
,
или 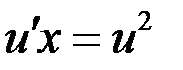 .
.
Это уравнение является дифференциальным уравнением с разделяющимися переменными. Решим его.
|
|
|
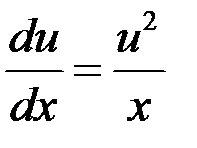 ,
, 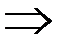
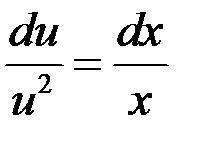 ,
, 
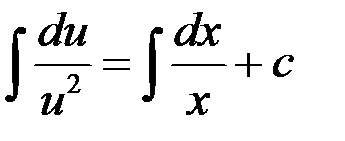 ,
, 
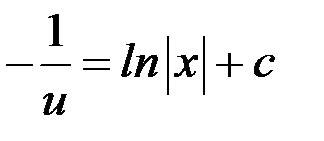 ,
, 
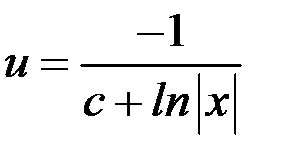 .
.
Найденное решение 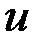 подставим в формулу
подставим в формулу 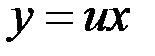 и получим, что общее решение исходного ДУ есть
и получим, что общее решение исходного ДУ есть 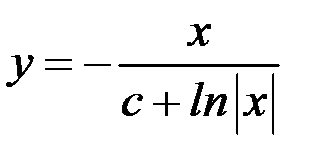 .
.
Пример 3. Найти общее решение дифференциального уравнения
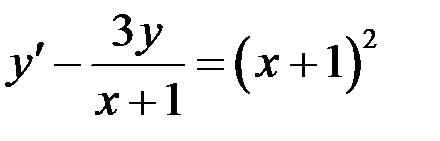 .
.
Решение. Данное уравнение является линейным ДУ первого порядка, то есть уравнением вида 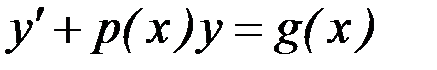 (здесь
(здесь 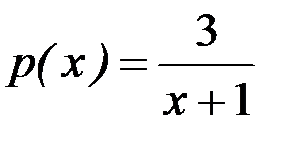 ,
, 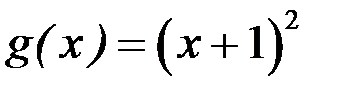 ). Его решение будем искать в виде произведения двух функций
). Его решение будем искать в виде произведения двух функций 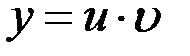 . Запишем производную произведения
. Запишем производную произведения 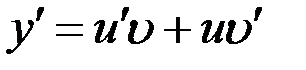 . Подставляя данные выражения в ДУ, получаем
. Подставляя данные выражения в ДУ, получаем
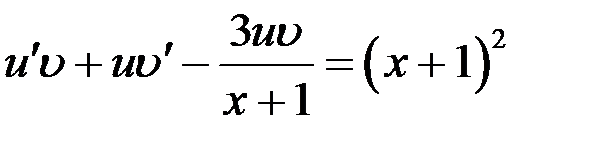
или 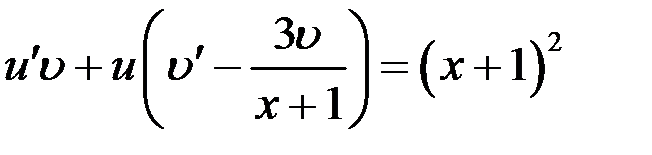 . (
. ( )
)
Приравняем к нулю выражение в скобках в левой части уравнения ( ):
):
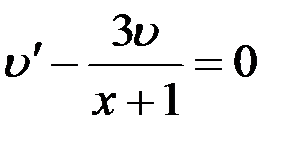 . Решив это ДУ с разделяющимися переменными, найдем функцию
. Решив это ДУ с разделяющимися переменными, найдем функцию 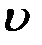 .
.
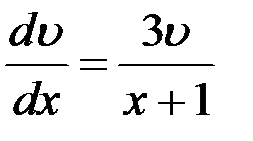 ,
,  ,
, 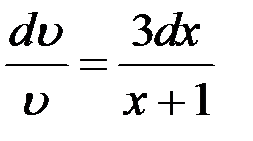 ,
, 
 ,
, 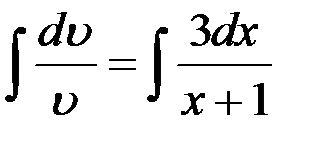 ,
,  ,
, 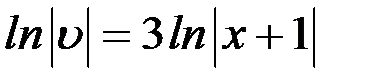 ,
, 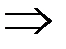
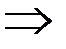 ,
, 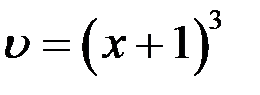 .
.
(Так как ищется любое ненулевое частное решение 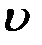 , то значение произвольной постоянной при интегрировании можно выбрать нулевым).
, то значение произвольной постоянной при интегрировании можно выбрать нулевым).
Подставив найденную функцию 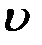 в равенство (
в равенство ( ), получаем
), получаем
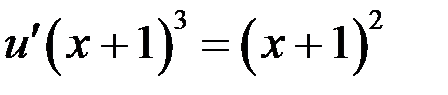 , или
, или 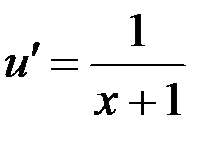 .
.
Полученное ДУ с разделяющимися переменными запишем в виде
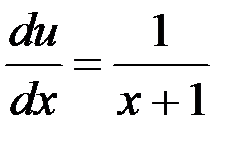 или
или 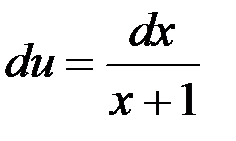 .
.
Интегрируя обе части последнего уравнения, получаем
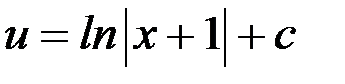 .
.
Перемножив найденные функции 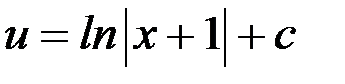 и
и 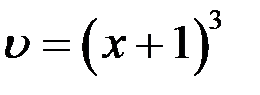 , получим общее решение исходного дифференциального уравнения
, получим общее решение исходного дифференциального уравнения
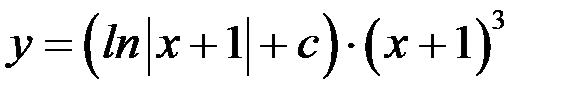 .
.
Пример 4. Найти решение задачи Коши для линейного однородного дифференциального уравнения второго порядка
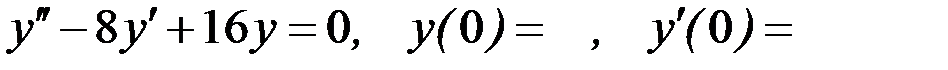
Пример 5. Найти общее решение линейного дифференциального уравнения второго порядка
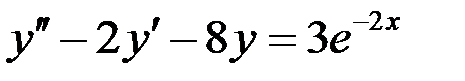 .
.
Решение. Общее решение линейного дифференциального уравнения второго порядка имеет вид 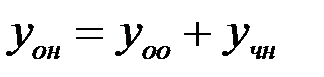 , где
, где 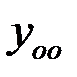 – общее решение однородного уравнения, а
– общее решение однородного уравнения, а 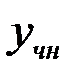 – частное решение неоднородного уравнения.
– частное решение неоднородного уравнения.
Сначала решим однородное уравнение
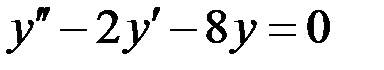 .
.
Составим для этого ДУ характеристическое уравнение
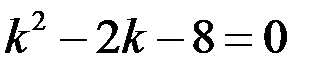 .
.
Решая это квадратное уравнение, находим его корни 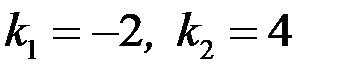 . Так как
. Так как 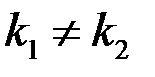 , то общее решение однородного ДУ имеет вид
, то общее решение однородного ДУ имеет вид
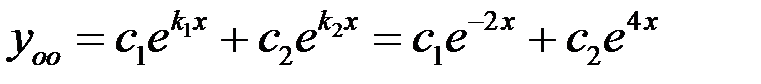 .
.
 2020-10-09
2020-10-09 191
191








