Категоричность теории натуральных чисел.
Непротиворечивость системы аксиом Пеано.
Независимость аксиом Пеано.
 Аксиома 3 не выполняется, т.к.
Аксиома 3 не выполняется, т.к.
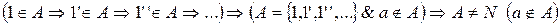 .
.
Система аксиом Пеано не является противоречивой, поскольку существует модель, на которой выполняются эти аксиомы.
Для доказательства категоричности достаточно показать, что две произвольные модели множества натуральных чисел изоморфны между собой.
Рассмотрим две произвольные модели 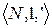 и
и 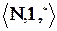 . Пусть соответствие
. Пусть соответствие 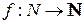 задано по следующим правилам:
задано по следующим правилам:
1. 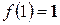 ;
;
2. 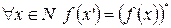 .
.
Покажем, что 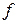 является биекцией. Тем самым и докажем изоморфизм моделей.
является биекцией. Тем самым и докажем изоморфизм моделей.
Всюду определенность (?)
 .
. 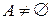 , т.к.
, т.к. 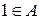 . Покажем, что
. Покажем, что 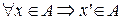 .
. 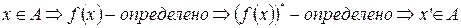 . Тогда, по 3 аксиоме Пеано,
. Тогда, по 3 аксиоме Пеано, 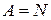 .
.
Однозначность (?)
Покажем, что 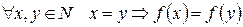 . Доказательство проведем методом математической индукции в І форме для натуральных чисел по
. Доказательство проведем методом математической индукции в І форме для натуральных чисел по 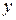 .
.
База индукции 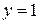 :
:
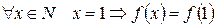 , т.е.
, т.е.  (?)
(?)
Предположим, что 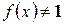 .
. 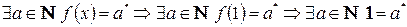 , последнее противоречит 1 аксиоме Пеано. Таким образом, предположение неверно.
, последнее противоречит 1 аксиоме Пеано. Таким образом, предположение неверно.
Индуктивное предположение  :
:
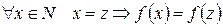 .
.
Покажем справедливость утверждения для 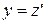 :
:
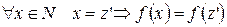 (?)
(?)
Предположим, что  .
.
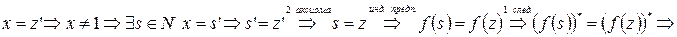
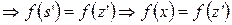 .
.
Итак, доказано, что 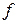 является отображением. Остается проверить сюръективность и инъективность
является отображением. Остается проверить сюръективность и инъективность 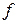 . Для чего рассмотрим следующую систему множеств:
. Для чего рассмотрим следующую систему множеств: 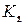 ,
, 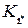 ,…,
,…, 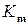 ,…, где
,…, где 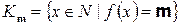 . Докажем методом математической индукции в І форме для натуральных чисел по
. Докажем методом математической индукции в І форме для натуральных чисел по 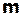 , что каждое из этих множеств непустое и одноэлементное, тем самым убедимся в сюръективности и инъективности
, что каждое из этих множеств непустое и одноэлементное, тем самым убедимся в сюръективности и инъективности 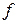 , соответственно.
, соответственно.
База индукции 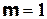 :
:
 (?)
(?)
Очевидно, что 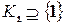 , т.к.
, т.к.  . Предположим, что
. Предположим, что 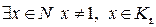 .
.
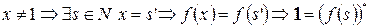 . Последнее противоречит 1 аксиоме Пеано, следовательно, предположение неверно.
. Последнее противоречит 1 аксиоме Пеано, следовательно, предположение неверно.
Индуктивное предположение  :
:
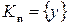 .
.
Покажем справедливость утверждения для  :
:
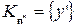 (?)
(?)
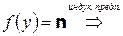
 . Предположим, что
. Предположим, что 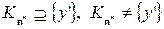 . Тогда
. Тогда 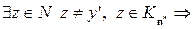
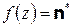 . Возможны случаи:
. Возможны случаи:
§ 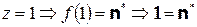 . Последнее противоречит 1 аксиоме Пеано.
. Последнее противоречит 1 аксиоме Пеано.
§ 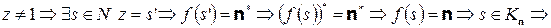
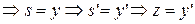 , что противоречит условию
, что противоречит условию 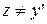 .
.
Таким образом, в обоих случаях получено противоречие, следовательно, предположение неверно.
что и требовалось доказать.
 2014-02-02
2014-02-02 1395
1395








