О моделях расчета конструкций

Расчеты и проектирование конструкций либо оценка их состояния – основная повседневная работа инженера-строителя. Используемую при этом систему моделей называют механикой твердых деформируемых тел (т.е. элементов конструкций). Она является частью механики сплошных сред (наряду с механикой жидкостей и газов, моделирующей водоснабжение, отопление, вентиляцию и др.). В нее входят сопротивление материалов, строительная механика, теории упругости, пластичности, ползучести и др.

Механика – наиболее очевидная и в то же время наиболее сложная модель окружающего нас мира, состоящая из многих многосторонних понятий и достаточно сложных связей между ними. Чтобы освоиться с ними, нужно, бегло познакомившись, придумать их для себя, проделав для этого многочисленные упражнения, как предложенные преподавателем и учебником, так и придуманные для себя в соответствии с достигнутым пониманием, нарисовав и обдумав многочисленные изображения этих понятий в разных ситуациях. Учитель может указать путь, а пройти его нужно самому, другого способа в моделировании нет. Этим достигается не только высокая квалификация в своей профессии, но и умение быстро переквалифицироваться, создавая в своем сознании новые понятия, аналогичные или, может быть, противоположные уже накопленным.

Геометрические понятия механики отражают видимую сторону поведения окружающих нас предметов. К ним относятся непрерывность (сплошность) среды и процессов, перемещения тел и их частей и их деформации, т.е. изменения формы.

Непрерывность определяют как бесконечную делимость: любая часть непрерывного объекта (тела или процесса) обладает такими же свойствами, как и весь объект. Стремясь к точному выражению этого свойства, наши предки придумали дробные (рациональные), а затем иррациональные и действительные числа, с помощью которых описывают время. пространство и связанные с ними свойства объектов внешнего мира. Эти свойства определяют непрерывными функциями от времени или координат (рис. 1, б). Заметьте, что в мысленном моделировании очень важно придумывать и накапливать в своей нейросети не только слова, имена понятий, но и наглядные образы (зрительные, звуковые и другие). Понятие имеет содержание, которое дается определением, выделяющие его среди других понятий, и объем ­– набор экземпляров, в сопоставлении с которыми оно потом узнается. «Мы не понимаем многие вещи не потому, что наши понятия слабы, а потому, что они не входят в круг наших понятий» (Козьма Прутков): чтобы расширить этот круг, нужны тренировки ­– нарабатывать объемы понятий.

Математический анализ – модель непрерывных процессов и сплошных сред. К математике при этом относят общие вопросы, выражающие собственные свойства мысленной модели, вне зависимости от того, какой реальный объект она моделирует: равновесие конструкции, движение воды в трубе, обтекание воздухом крыла самолета или распространение электромагнитного поля. В матанализе объект исследования – непрерывная функция (например, y_A (t) на рис. 1). В чем сложность этого объекта? Подсчитайте, сколько чисел его определяет: y_A (0), y_A (1), y_A (0.5), … – бесконечно много. (сравните: вектор на плоскости определяется парой, в пространстве – тройкой чисел). Как вычислять бесконечные наборы чисел? Риторический вопрос: никак нельзя. Бесконечные модели предназначены для приближенных расчетов, и это не нужно относить к ее недостаткам, так как все равно любая модель (и мысленная математическая, и реальная физическая) лишь приближенно представляет свой объект.

А есть ли в окружающем мире такие идеально сплошные объекты? ­– Нет, конечно: все знают средний размер молекулы (около 10^–22 см), и время в микромире тесно связано с пространством и имеет свои дискретные свойства. Тогда зачем бесконечная делимость? А это нужно для упрощения рассуждений. Здесь применяют стандартный прием моделирования – абстракцию: отвлекаются от особых свойств представителей некоторого класса объектов, чтобы подробнее разобраться в их общих свойствах. Никто не собирается, применяя бесконечномерную модель, делить ее на 10²² частей, никакой компьютер это в принципе не потянет.

Очень сложные объекты исследования у математического анализа. По смыслу слова «анализ» основной метод исследования связан с разделением сложного объекта на более простые части (рис. 2). Однако подсчитаем, насколько проще часть функции f(x) на малом отрезке dx проще, чем f(x) на всем интервале [ a, b ]: f*₁, f*₂, f*₃,… – тоже бесконечное множество значений: ничем не проще. Здесь не обойтись без приближенной замены f(x) на участке dx на более простую функцию. Самая простая функция – константа y = c, все ее бесконечное множество значений выражается через одно число. Такое приближение используют иногда при вычислении интегралов. Линейная функция y = ax + b самая ходовая в анализе, она тоже простая, определяется двумя числами и вычисляется самыми простыми арифметическими действиями, и в то же время достаточно сложная, чтобы разобраться в большинстве вопросов, возникающих при исследовании сплошных сред и непрерывных процессов. Вспомните: главный коэффициент a в этом линейном приближении называют производнойf’(x). Нередко используют многочлены более высокой степени, они определяются конечными наборами своих коэффициентов и вычисляются простыми действиями.

Таким образом, основной метод математического анализа – это разделение на малые части и на каждой из них приближенная замена исходной сложной функции на более простую. Такая замена на малых частях обосновывается тем, что непрерывные функции обычно плавно меняются, и в анализе много усилий посвящают определению условий применимости или неприменимости такой замены.

Геометрические понятия механики – перемещения и деформации. Точка на плоскости или в пространстве может перемещаться в любом из бесконечного числа направлений. Но, следуя Рене Декарту (1596 – 1650), в расчетах это изображают парой или тройкой чисел – проекций вектора перемещений на выбранные исследователем координатные оси (рис. 3, а).

Элемент конструкции или любое другое твердое тело состоит из бесконечного количества точек, так что его перемещение определяется бесконечным набором их векторов перемещений – полем перемещений (рис. 3, б). Такое сложное понятие не изобразишь одним рисунком, нужно найти разные точки зрения (рис. 3, в, г, …).

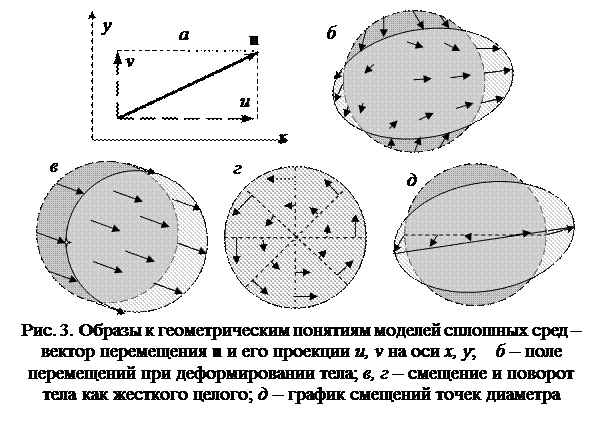При этом взаимное расположение точек может не изменяться (перемещение тела как жесткого целого) или изменяться (тогда говорят об изменении формы, или деформации).

Вычислительные (математические, мысленные) модели строят для получения информации – для расчета. Относительно всех понятий нужно придумать, как их измерить, как выразить числом. Ясно, что поле векторов перемещений (на плоскости) представляет собой набор векторов (т.е. пар их координат) u (x, y) = (u (x,y), v (x,y)), определенных в точках тела, так что после деформирования x* = x+u(x, y) и y*=y+v(x,y). Это векторное поле полностью определяет изменение формы тела и любой его части. Но в нем содержатся и перемещения тела как жесткого целого.

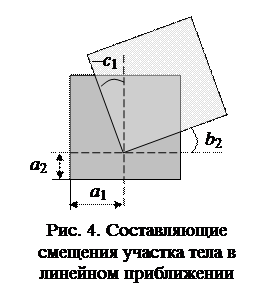Деформации тела могут быть сложными и самыми разнообразными, одним числом это не выразишь. Чтобы в них разобраться и использовать в расчетах, применяют основной метод анализа: разделение объекта исследования на малые части и приближенную замену его простыми, линейными объектами. Деформацию тела представляют себе и изображают как совокупность деформаций малых окрестностей точек, в которых зависимости перемещений от координат представляют линейными функциями (следуя Исааку Нютону, 1647 – 1727)[1]

u(x, y) = a ₁ +b ₁ x + c ₁ y, u(x, y) = a ₂ +b ₂ x + c ₂ y. (1)

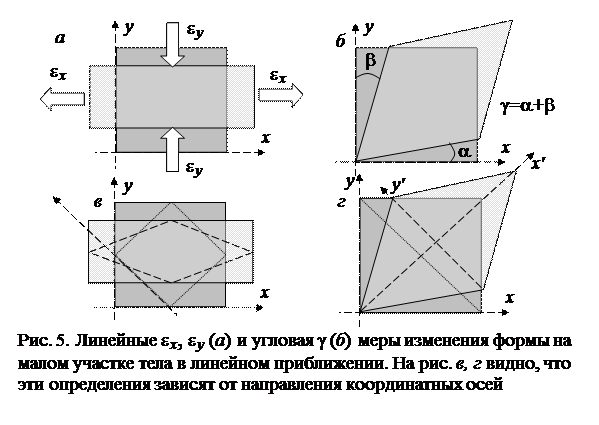
Здесь коэффициенты a ₁, a ₂и комбинация w = c ₁– b ₂ представляют смещение выбранного малого участка как жесткого целого (рис. 3), а e _x = b ₁, e _y = c ₂ и g_xy = c ₁+ b ₂ – меры изменения формы (деформации) этого участка в первом (линейном) приближении (рис. 5). Так как коэффициенты b ₁, c ₁, b ₂, c ₂, по определению, представляют собой производные от функций u и v, то можно написать объясненное выше определение локальных мер деформации в окрестности точки (x, y) как

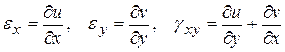. (2)

Таким образом, на плоскости деформация малого участка определяется тремя числами – два относительных удлинения (рис. 5, а) и один угол сдвига (рис. 5, б). Линейные и угловые деформации взаимосвязаны, например относительные удлинения в одних координатах превращаются в углы сдвига в системе координат, повернутой на 45° (т.е. смотря с какой стороны смотришь). Можно, например, за меру изменения формы взять три относительных удлинения в трех разных направлениях (в пространстве шесть).

На самом деле относительных удлинений и углов сдвига одного малого участка бесконечное множество (линейные деформации во всех направлениях и угловые – между любыми двумя осями), но все они выражаются через три основных меры деформации на плоскости или шесть основных – в пространстве.

В пространстве изменение формы окрестности точки в линейном приближении представляют шестью числами: три линейных деформации (относительные удлинения в трех координатных направлениях) и три угловых деформации (углы сдвига между парами координатных осей), через которые можно выразить относительные удлинения и углы сдвига в других направлениях.

Понятия перемещений и деформаций составляют геометрическую сторону задачи механики твердого деформируемого тела, а связь между ними (2) – геометрические уравнения. Это видимые, наблюдаемые и измеряемые понятия, и наши представления о них легко формируются и уточняются.

Статические понятия – силы и их действие на тела – относятся к неочевидным понятиям механики. Представления о них возникли в связи с тем, что тела (как твердые, так и жидкие и газообразные) сопротивляются внешним воздействиям со стороны других тел или физических полей (гравитационных, электромагнитных). Измерить эту воображаемую величину можно только косвенно, по результатам ее воображаемого действия на пружину динамометра (т.е. по вызываемой ей деформации) или сравнивая с действием силы тяжести на эталонную массу (на рычажных весах), т.е. выразить через деформацию или массу эталона.

Силы всегда распределены по поверхности (давление воды, ветровые, снеговые нагрузки и др.; внутренние силы) или объему (собственный вес, электромагнитные силы). Не могут существовать сосредоточенные воздействия: никакой материал не выдерживает бесконечных напряжений, и сила тут же исчезает. Называя силу сосредоточенной, в механике отвлекаются (абстрагируются) от величины площади или объема, на которых она распределена, и хотят в своей (приближенной) модели использовать только величину равнодействующей силы, назначив ей наиболее подходящую точку приложения (рис. 6, 7)..

При моделировании поведения конструкции исходят из того представления, что при приложении нагрузки она приходит в движение, при этом ее материал деформируется и в нем возникают внутренние силы упругого взаимодействия материальных частиц, действующие на соседние частицы и ускоряющие их. Движение постепенно останавливается из-за рассеивания энергии деформирования в материале (из-за перехода ее в тепловую энергию молекул), и наступает покой ­ равновесие между внутренними и внешними силами. Поэтому самое распространенное применение модели конструкции – статический расчет, т.е. решение задачи о равновесии: какие внутренние силы должны возникнуть, как они должны распределиться по конструкции, чтобы любая ее часть находилась в равновесии. Равновесие тел наступает тогда, когда суммарная сила, действующая на каждую его часть, равна нулю (рис. 8, 9). Таким образом получают первое приближение к оценке прочности на основе имеющихся данных о прочностных свойствах материала.

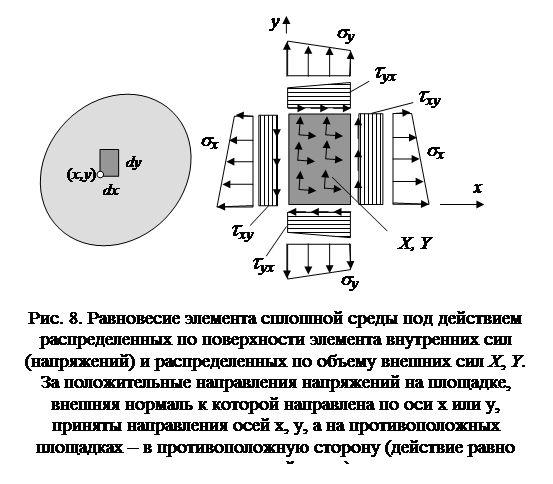Подсчитывая и складывая компоненты равнодействующих внутренних сил на всех сторонах выделенного малого объема (рис. 8) и равнодействующей внешней объемной силы (X, Y), составляют уравнения равновесия этого объема:

SX = s_x (x, y+dy /2) dydz – s_x (x+dx, y+dy /2) dydz +

t_yx (x+dx/2, y) dxdz – t_yx (x+dx/2, y+dy) dxdz +

t_zx (x+dx/2, y) dxdy – t_zx (x+dx/2, y+dy) dxdy + X dx dy dz = 0.

Второе и третье уравнения равновесия (SY и SZ) составьте сами. На рис. 8 не показана ось Z и перпендикулярные к ней площадки выбранного малого объема (отсеченной части). Изобразите сами трехмерную отсеченную часть и напряжения на площадках всех трех направлений, используйте уточненное изображение для более надежного, безошибочного получения зависимостей между понятиями статической модели.

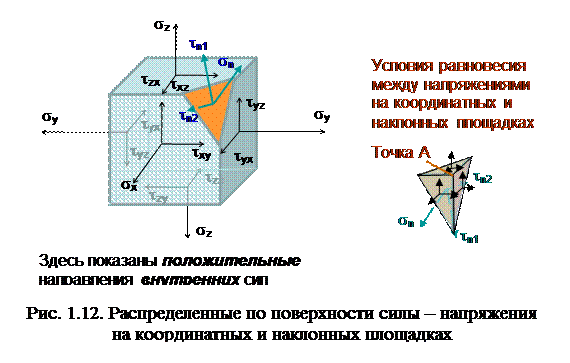В трехмерном пространстве совокупность внутренних сил в одной точке изображают параллелепидом (рис. 1.12): на таком рисунке видно, какие силы относятся к каким площадкам, проходящим через точку А. Нельзя все девять компонентов трех векторов напряжений показать в одной и той же точке A, их приходится раздвинуть в центры граней параллелепипеда. Кроме того, на этом же вырезанном их объема малом параллелепипеде удобно показать положительные направления внутренних сил (напряжений) на противоположных гранях в соответствии с аксиомой о действии и противодействии.

Для моделирования движения делают небольшое дополнение к рассуждениям о равновесии (см. ниже).

Чем отличаются внутренние силы от внешних? – Внутренние силы – это взаимо действие. А разве, например, сила тяжести – не взаимодействие? Силы – всегда взаимодействие. А внешняя сила – относительное понятие, относительно рассматриваемой отсеченной части. Рассматривая конструкцию, мы «отсекаем» ее от гравитационного поля Земли и от воздуха, который на нее давит, и от других взаимодействующих с ней объектов, и силы взаимодействия с этими объектами называем внешними по отношению к рассматриваемому объекту (конструкции).

Физические понятия (упругость, пластичность и др.) – это представления о взаимосвязи сил и деформаций, статических и геометрических величин. Такие взаимосвязи зависят от свойств материалов и составляют, как принято говорить, физическую сторону модели. Модели конструкций – твердые деформируемые тела – отличаются от моделей сплошных сред с другими физическими свойствами – жидкостей и газов – физическими уравнениями, связывающими между собой силы и деформации. Если для жидкостей и газов характерны зависимости между силами и скоростями деформирования, то для твердых тел – между силами и величинами деформаций.

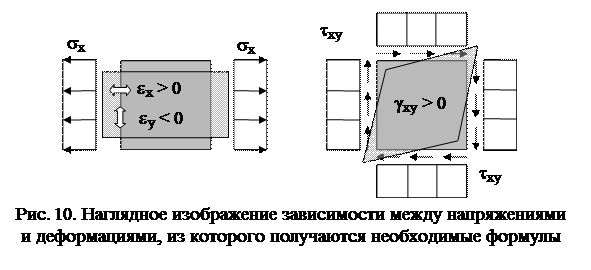
Простейшая физическая модель элемента конструкции – упругое тело, в нем деформации взаимно однозначно связаны с силами (точнее, с напряжениями), так что при снятии нагрузки оно принимает исходную форму. Почти все конструктивные материалы до какого-то предела нагрузки при малом времени воздействия ведут себя упруго, а при не слишком больших нагрузках ­– линейно упруго, согласно закону Гука. При этом, например, продольные (нормальные) растягивающие силы вызывают не только продольные деформации (увеличение длины), но и поперечные деформации (уменьшение толщины), так как материал сопротивляется изменению объема (рис. 10, а). В результате (для изотропного материала) часть закона Гука, связывающая линейные деформации с нормальными напряжениями, имеет вид

e_x = E (s_x–ms_y–ms_z), e_y = E (s_y–ms_z–ms_x), e_z = E (s_z–ms_x–ms_y),

где коэффициент Е определяет жесткость материала на растяжение и сжатие и носит название модуля упругости или модуля Юнга, а коэффициент Пуассона m (0£m£0.5)показывает, какую долю от продольной деформации e_x составляют поперечные деформации e_y, e_z (имеющие противоположный знак) при действии продольной нагрузки s_x. Если m=0, материал не изменяет поперечных размеров при приложении продольной нагрузки. Если m=0.5, материал несжимаемый, при любых нагрузках не изменяет объема. К несжимаемым материалам относят, например, резину.

Другая часть этого закона связывает угловые деформации с вызывающими их касательными напряжениями (рис. 10, б):

t_xy = G g_xy, t_yz = G g_yz, t_xz = G g_xz,

здесь коэффициент G называют сдвиговой жесткостью или модулем сдвига. Для изотропного материала G = E / 2(1+m).

Под действием больших сил одни из материалов разрушаются (камень, бетон, стекло), другие переходят в пластичное состояние (металлы, пластмассы).

При моделировании разрушения исходят из опыта, который показывает, что в хрупкие материалах при растяжении возникают трещины. Например, прочность бетона на растяжение составляет 1 – 1.5 МПа, на сжатие 15 –120 МПа. При более подробном анализе выясняется, что при всестороннем растяжении напряжение трещинообразования значительно выше, а наиболее опасно сочетание растяжения в одном направлении со сжатием в другом. Так как касательные напряжения в одной системе координат соответствуют сочетанию растяжения со сжатием в другой системе координат (повернутой на 45°, рис. 10), то за критерий прочности материала принимают максимальное касательное напряжение или пропорциональные ему величины, 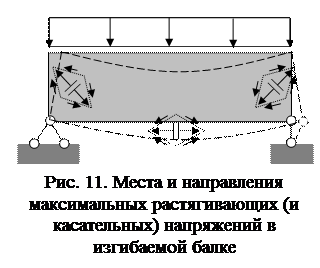соответствующие предельному растягивающему напряжению в эксперименте на растяжение стержня. Задача прочности состоит в том, чтобы определить, в какой точке, на какой площадке и в каком направлении действует максимальное касательное напряжение или, в зависимости от особенностей задачи, максимальная деформация сдвига (рис. 11).

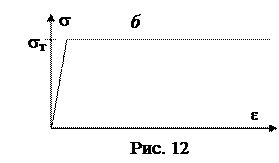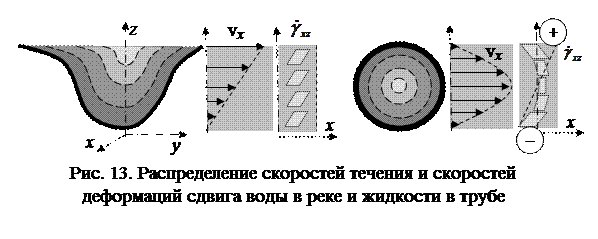
Металл при небольших нагрузках ведет себя упруго, но при превышении некоторого напряжения текучести в нем происходят необратимые (пластические) деформации (рис. 12, а): при снятии нагрузки тело не возвращается в исходное положение, остаются остаточные деформации (вы когда-нибудь гнули проволоку?). Это упруго-пластичный материал. При чем здесь текучесть – в твердом теле? Представьте себе, как течет вода под действием силы тяжести по наклонному руслу реки или под действием разности давлений по трубе (рис. 13). Внешний слой «прилип» к дну реки или к стенке трубы. Упомянутые силы вызывают в нем деформации сдвига g (внутреннего слоя по отношению к внешнему), которым вода не сопротивляется. Но она сопротивляется изменению деформации сдвига 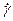, причем сила сопротивления пропорциональна 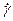, т.е. скорости изменения g. Поэтому внутренние слои тормозятся о внешние, увлекая их за собой, и центральный слой имеет самую высокую скорость. Сплавляясь на плоту, замечали, что у левого берега он вращается против часовой стрелки, а у правого – по часовой стрелке? Нарисуйте вид сверху поверхности реки, придумайте, как изобразить скорости течения и на этой модели увидеть направление вращения плота.

А знаете, как сплавщики леса с помощью весел управляют огромными плотами из бревен? Они разворачивают плот в сторону того берега, к которому хотят его направить (рис. 14). Скорость плота, как самого верхнего слоя в этой системе на наклонной плоскости, выше, чем скорость окружающей воды, а из-за большой длины он значительно легче движется вдоль своей оси, чем поперек. За счет этого для перемещения плота к правому или левому берегу реки удается использовать энергию силы тяжести. Вспомните родственный технический прием: плавание на парусном судне против ветра за счет
смены галсов (рис. 15).

Из подобных наблюдений складываются свойства жидкостей, составляющие их математическую модель. Основное из них – зависимость (в первом приближении – линейная) скорости деформаций сдвига от касательных напряжений. Течение ­– сугубо динамический процесс, он зависит как от пластических свойств жидкости (сопротивления изменению угловых деформаций), так и от плотности материала (сопротивления ускорениям).

Пластические свойства металлов и других твердых материалов подобны свойствам текущей жидкости, отсюда и названия «текучесть», «теория течения» в моделях пластического деформирования. Разница в том, что вода не обладает упругими свойствами по отношению к деформациям сдвига и касательным напряжениям, совсем не сопротивляется деформациям сдвига, она – идеально пластический материал.

Вспомните, что для построения вычислительной модели деформирования сплошное тело мысленно разделяют на малые части, на каждой из которых, исходя из линейного приближения для поля перемещений, определяют меру изменения формы в виде набора из шести чисел, называемого тензором деформаций

.

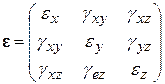При моделировании пластического или упруго-пластического деформирования шесть компонентов тензора e приходится делить на две составляющих: «шаровой» тензор объемных деформаций, характеризующий всестороннее растяжение или сжатие (относительное изменение объема в линейном приближении)

, где e ₀ = e_x + e_y + e_z

и девиатор тензора e, характеризующий деформации без изменения объема

.

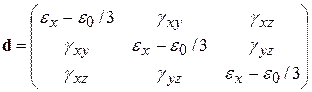Здесь тензор e ₀определяется одним числом, а в d содержится пять независимых чисел, так как определитель матрицы d равен нулю, т.е. в e ₀ и d информации об изменении формы ровно столько же (6 чисел), сколько в исходном тензоре деформаций e.

Обычно при нагрузках всестороннего сжатия или растяжения материал деформируется упруго, т.е. после снятия нагрузки восстанавливает исходный размер. Зато при угловых деформациях (или, что примерно то же самое, при растяжении в одних направлениях и сжатии в других) уже при значениях g @ 0.001 в металлах начинается необратимое течение, а в однонаправлено сжатом бетоне – разрушение.

Ярко выраженные пластические деформации и их «сдвиговая» основа наблюдаются при резании металлов.

Чтобы определить начало течения или разрушения материала в данной точке, исследуют деформации сдвига на площадках разных направлений и выбирают максимум. Или находят направления главных деформаций (максимальной и минимальной) и по их разности судят о начале неупругой работы материала.

Так как это нужно проделывать в каждой точке, то вы можете себе представить, что модель поведения конструкций под нагрузкой непростая и усваивается не сразу, а при многократном выполнении различных упражнений. Особенности всех понятий постепенно накапливаются и связываются между собой. Некоторые наиболее простые упражнения в этой области присутствуют и в вашем курсе информатики. Основную информацию строителя-конструктора составляют понятия внутренних и внешних сил, упругого и неупругого деформирования, расчетного сопротивления материала, запаса прочности, предельного равновесия, ползучести материалов и релаксации напряжений в них и др.

Ползучестью материала называют явление возрастания деформаций со временем при постоянной нагрузке. Это явление вполне ожидаемое (конструкция не сразу принимает окончательную равновесную форму), но в металлах и бетоне оно медленное и обнаруживается длительными наблюдениями. Ползучесть, как и пластичность, связывают с деформациями сдвига, отделяя их от изменения объема.

Если вы сильно сжали бетонный элемент и закрепили его в таком положении, то за длительное время в нем должна происходить ползучесть, однако деформации в этих условиях не могут изменяться. Явление ползучести здесь выражается в том, что напряжения в материале постепенно уменьшаются. Этот процесс изменения напряженного состояния материала называю релаксацией напряжений, т.е. их ослаблением с течением времени. Релаксация – это ползучесть при других условиях закрепления образца.

Ползучесть и релаксацию называют реологическими явлениями, которые отражают реологические свойства материала, т.е. свойства, изменяющиеся со временем.

2. Простейшая модель сплошной среды –

Распространение тепловой энергии (теплопередача)

2.1. Моделирование одномерных (1D – one-dimensional)