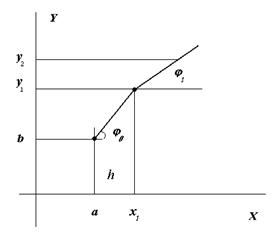
Геометрический смысл метода Ньютона (метода касательных) заключается в том, что на отрезке 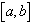 содержащем корень уравнения (1) график функции
содержащем корень уравнения (1) график функции 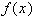 заменяется отрезком касательной, проведенной к графику
заменяется отрезком касательной, проведенной к графику 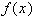 при
при 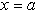 или
или  . (Предполагая что функция
. (Предполагая что функция 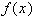 дифференцируема на
дифференцируема на 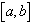 .)
.)
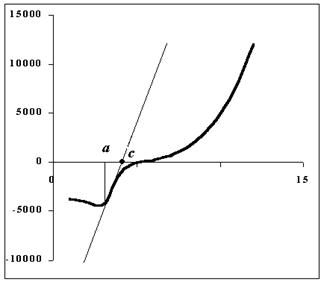
При этом используется только одна точка, поэтому не обязательно задавать отрезок 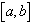 , содержащий корень, достаточно задать некоторое приближение
, содержащий корень, достаточно задать некоторое приближение 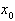 .
.
Уравнение касательной в точке 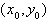
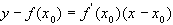 .
.
Для точки пересечения с осью 0x получаем
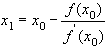 , и т. д.
, и т. д.
Объем вычислений в методе Ньютона на каждом шаге выше, чем в предыдущих методах, т. к. в точке 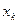 вычисляются значения функции и ее производной, что компенсируется более высокой скоростью сходимости этого метода.
вычисляются значения функции и ее производной, что компенсируется более высокой скоростью сходимости этого метода.
Но в отличие от предыдущих методов метод Ньютона сходится не при всяком выборе начального приближения на отрезке, содержащем корень уравнения. Сходимость имеет место тогда, когда для начального значения 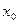 выполняется неравенство
выполняется неравенство 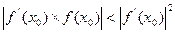
При этом последовательные приближения будут сходится к корню монотонно.
3. Квадратурные формулы.
Постановка задачи численного интегрирования.
Пусть требуется вычислить
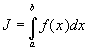
Если 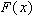 - первообразная для
- первообразная для 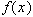 , то
, то 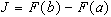 . Часто получить выражение для первообразной не удается. Подынтегральная функция может быть задана в табличном виде. В этих случаях подынтегральную функцию заменяют на некоторую аппроксимирующую функцию, интеграл от которой легко вычисляется в элементарных функциях. Во многих случаях формулы для приближенного вычисления интегралов можно записать в виде
. Часто получить выражение для первообразной не удается. Подынтегральная функция может быть задана в табличном виде. В этих случаях подынтегральную функцию заменяют на некоторую аппроксимирующую функцию, интеграл от которой легко вычисляется в элементарных функциях. Во многих случаях формулы для приближенного вычисления интегралов можно записать в виде
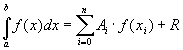
Формулы такого вида называются квадратурными.
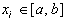 - узлы квадратурной формулы.
- узлы квадратурной формулы.
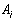 - коэффициенты.
- коэффициенты.
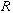 - погрешность (остаточный член) квадратурной формулы.
- погрешность (остаточный член) квадратурной формулы.
Формула прямоугольников.
Допустим, что 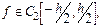
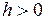 . Положим приближенно
. Положим приближенно
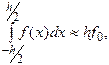 (3)
(3)
где 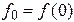 , т.е. площадь криволинейной трапеции, ограниченной сверху графиком функции
, т.е. площадь криволинейной трапеции, ограниченной сверху графиком функции 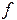 , аппроксимируется площадью прямоугольника, высота которого равна значению
, аппроксимируется площадью прямоугольника, высота которого равна значению 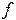 в средней точке основания трапеции.
в средней точке основания трапеции.
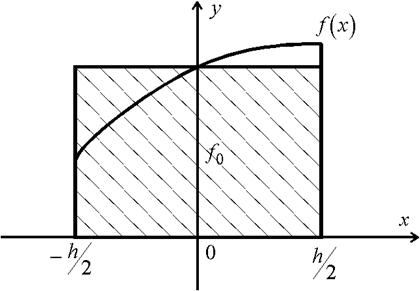
Погрешность формулы (3) для этого случая,
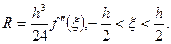
Формула трапеций.
Пусть 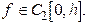 Полагаем
Полагаем
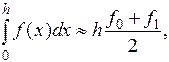 (4)
(4)
 где
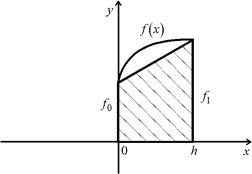
где 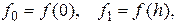 т.е. интеграл
т.е. интеграл 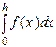 приближенно заменяется площадью заштрихованной трапеции, показанной на рисунке.
приближенно заменяется площадью заштрихованной трапеции, показанной на рисунке.
Погрешность формулы (3) для этого случая,
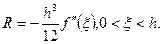
Формула Симпсона.
Предположим, что 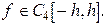 Интеграл
Интеграл 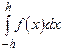 приближенного заменяем площадью заштрихованной криволинейной трапеции, ограниченной сверху параболой, проходящей через точки
приближенного заменяем площадью заштрихованной криволинейной трапеции, ограниченной сверху параболой, проходящей через точки 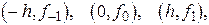 де
де 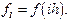
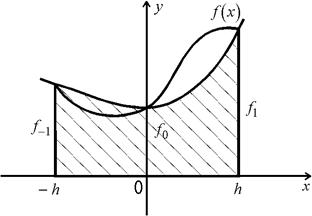
Указанная парабола задается уравнением
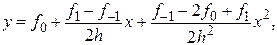
в чем нетрудно убедиться, положив поочередно 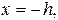
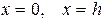 . Отсюда находим
. Отсюда находим
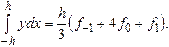
Таким образом, формула Симпсона, называемая также формулой парабол, имеет вид
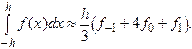
Погрешность формулы для этого случая,
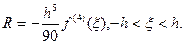
4. Имеется большое число частных случаев дифференциальных уравнений, которые можно проинтегрировать в конечном виде; однако большинство задач с дифференциальными уравнениями может быть решено только численно. Простейшим методом решения является метод Эйлера, легко реализуемый графически.
 2014-02-10
2014-02-10 1346
1346








