Матрица рисков Табл. 3
M
Критерий Байеса (критерий ожидаемого значения).
Задача принятия решений в условиях риска
Методы и модели анализа и принятия решений в условиях риска
Задача принятия решений в условиях риска. Критерий Байеса (критерий ожидаемого значения). Модальный критерий (наиболее вероятного исхода). Критерий максимизации вероятности распределения ОФ. Критерий минимума дисперсии оценочного функционала
При анализе задач принятия решений в условиях риска (стохастических ЗПР) предполагаются заданными:
1)множество решений А={ai}k, одно из которых может принять ЛПР;
2)множество ситуаций S={sj}k, в одной из которых будет находиться среда в момент реализации выбранного решения;
3)оценочный функционал F, элементы которого представляют собой количественную оценку полезности исходов решений;
4)вероятности Рj=Р(s=sj), j=1,...,m ситуаций (состояний "природы"), P1+P2+...+Pm = 1.
Пример:F=F+
Табл. 1
| Решения | S1 | S2 | S3 | S4 |
| а1 | ||||
| а2 | ||||
| а3 | ||||
| Рj | 0.1 | 0.2 | 0.5 | 0.2 |
При решении ЗПР в условиях риска используются четыре основных критерия (правила), каждый из которых отображает особый подход к логическому обоснованию выбора решения: критерий Байеса; модальный, максимизации вероятности распределения оценочного функционала; минимума дисперсии оценочного функционала.
|
|
|
Кроме того, могут использоваться комплексные критерии (подходы) к определению предпочтительного решения. Различные критерии принятия решения в одних и тех же условиях могут иногда приводить к выбору различных решений.
Название этого критерия связано с именем математика Томаса Байеса (18 в.).
Критерий Байеса основывается на концепции "оптимизации в среднем", в соответствии с которой оптимальным является решение, максимизирующее средний "выигрыш" (или минимизирующее средний "проигрыш") ЛПР с учетом заданных вероятностей состояний среды. Сущность критерия состоит в максимизации математического ожидания ОФ при F+ (или минимизации ОФ при F-). Для каждого решения аi определяется "Байесово значение"
В (р,аi)= å рj *fij = (р1* fi1 +...+ рj *fij +...+рm *fim)
j=1
Оптимальным считается такое решение аo, дл0я которого выполняется:
В(р,аo)= max В(р,аi), при F = F+
и
В(р,аo)= min В(р,аi), если F = F-
Т.о. в соответствии с критерием Байеса выбирается решение, имеющее максимальное математическое ожидание, если ОФ выражает "выигрыши", "доходы", и минимальное математическое ожидание, если ОФ выражает потери, затраты и т.п.
Пример:F=F+ Табл. 2
| Решения | S1 | S2 | S3 | S4 | В(р,аi) |
| а1 | 5,2 | ||||
| а2 | 4,5 | ||||
| а3 | 5,0 | ||||
| Рj | 0.1 | 0.2 | 0.5 | 0.2 |
1) Вычисляем байесовы значения ОФ В(р,аi) для всех аi из А:
|
|
|
В (р,а1)= 0,1*1+0,2*4+0,5*5+0,2*9 = 5,2
В (р,а2)= 0,1*3+0,2*8+0,5*4+0,2*3 = 4,5
В (р,а3)= 0,1*4+0,2*6+0,5*6+0,2*2 = 5,0
2) Результаты расчета сведены в графу В(р,аi) таблицы 2.
3) ОФ F=F+, поэтому оптимальным по критерию Т.Байеса ("байесовским решением") является решение а1 с математическим ожиданием В(р,а1)= 5,2.
При выборе оптимального решения можно исходить не только из условия максимизации среднего выигрыша, но и минимизации среднего риска.
Решение, максимизирующее средний выигрыш, совпадает с решением, минимизирующим средний риск R(р,аi):
R (р,аi) = (р1*ri1 +...+ рj*rij +...+рm*rim)
Покажем это для условий примера, заданного табл.1. Для этого построим матрицу рисков и определим значения R(р,аi)
| Решения | S1 | S2 | S3 | S4 | В(р,аi) |
| а1 | 1,6 | ||||
| а2 | 2,3 | ||||
| а3 | 1,8 | ||||
| Рj | 0.1 | 0.2 | 0.5 | 0.2 |
R (р,а1)= 0,1*3+0,2*4+0,5*1+0,2*0 = 1,6
R (р,а2)= 0,1*1+0,2*0+0,5*2+0,2*6 = 2,3
R (р,а3)= 0,1*0+0,2*2+0,5*0+0,2*7 = 1,8
Оптимальным является решение а1 с ожидаемым риском R(р,а1)= 1,6. Таким образом, решение, обеспечивающее максимизацию среднего "выигрыша", совпадает с решением, минимизирующим средний риск.
Для двух ситуаций S ={S1, S2} выполняется p(S1)= 1- p(S2). В этом случае ЗПР с использованием критерия Байеса может решаться графическим методом. Рассмотрим пример
| Решения | S1 | S2 |
| а1 | ||
| а2 | ||
| а3 | ||
| Рj | p | 1-p |
Графический метод решения состоит в следующем.
1) Для a1 и a2 в координатах p - В(р,а1) строятся прямые
В(р,а1) = p*f11 + (1-p)*f12 = p*(f11-f12)+f12,
В(р,а2) = p*f21 + (1-p)*f22 = p*(f21-f22)+f22
В(р,а3) = p*f31 + (1-p)*f32)= p*(f31-f32)-f32
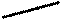
2) Определяется функция В(р) = max [В(р,аi)]
|
   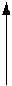 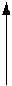
| |||||
    8 8
| |||||
    6 6
| |||||
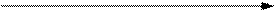
|
0 P1 P2 P=1
Рис.
Если вероятность р находится в интервале [0,P1], то оптимальным по Байесу является решение а1, если в диапазоне [P1,P2]- решение а3, в диапазоне [Р2,1] - решение а2.
Множество P(аi) значений вектора априорных вероятностей, для которого оптимальным по Байесу решением является аi, называется "байесовым множеством априорных вероятностей для решения аi". Для рассматриваемого примера
P(а1)= [0,P1]; P(а2)=[P2,1]; P(а3)=[P1,P2].
Критерий Байеса обеспечивает получение максимального среднего (ожидаемого) выигрыша. Использование ожидаемых значений ОФ предполагает возможность многократного решения одной и той же задачи и его применение обосновано тогда, когда одно и то же решение приходится принимать достаточно большое число раз. Для решений, которые принимаются редко, ориентация на критерий Байеса может приводить к неверным результатам.
Популярность критерия Байеса обусловливается тем, что он является наиболее обоснованным в теоретическом плане и полностью соответствует концепции теории рационального поведения Неймана-Моргенштерна (принципу максимизации ожидаемой полезности).
Модальный критерий (критерий наиболее вероятного исхода)
ЛПР исходит из того, что среда будет находиться в наиболее вероятном состоянии. В этом случае целесообразно рассматривать эффективность наиболее вероятных исходов решений, т.е. тех исходов, которые будут иметь место при наиболее вероятном состоянии среды.
Оптимальным считается решение, которому соответствует максимальное значение ОФ для наиболее вероятной ситуации.
Для примера табл. 1 наиболее вероятна ситуация S3 с Р3=0.5. Оптимальным является решение а3, поскольку для ситуации S3
f33= max {f13,f23,f33} = 6
Преимущества модального критерия определяются тем, что:
- для определения оптимального решения достаточно определить только наиболее вероятные ситуации, не уточняя при этом их численных значений,
- расчет ОФ может быть произведен только для самых вероятных ситуаций,
- выбор решения может осуществляться на основе анализа профиля предпочтений ЛПР без их количественной оценки.
|
|
|
Применение такого критерия не обосновано в тех случаях, когда множество состояний среды велико, а вероятности каждого из состояний малы.
 2014-02-13
2014-02-13 1522
1522








