Случайные погрешности

Случайные ошибки, как мы уже говорили, вызываются одновременными действиями очень большого числа факторов. Влияние каждого из них невелико, оно может изменяться хаотично или по какому-либо закону, поэтому суммарные действия всех факторов совершенно хаотично.

В каждом конкретном наблюдении случайная ошибка δх непредсказуема ни по знаку, ни по величине, однако, она подчиняется статическим закономерностям. Они проявляются при большом числе наблюдений.

Предположим, что проводится измерение некоторой величины х. Пусть систематические погрешности малы и ими можно пренебречь. Для надежной оценки случайных ошибок получены результаты х₁, х₂, …, х_n (n -наблюдений). Наиболее вероятное значение измеряемой величины (результат) определяется из (1.3).

Случайное отклонение результата i -го наблюдения от среднего 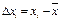может быть большим и малым, положительным или отрицательным, однако, чем больше отклонение, тем оно встречается реже и распределение Δ x_i будет симметричным относительно нулевого значения (рис. 1.1).

При этом оказывается, что приблизительно в 68% случаев отклонения |Δ x_i | не превышают некоторую величину σ называемую стандартным отклонением, а 32% превышают её. Иначе говоря, с вероятностью 68% отклонение х_i лежит в интервале [- σ; σ]. Для интервала [-2 σ; 2 σ ] эта вероятность составляет 95%, а для [-3 σ; 3 σ ] – 99,7% (рис. 1.1). Соответственно, для любой вероятности Р доверительный интервал [- λ_Pσ; λ_Pσ ] определяется числовым множителем λ_P зависящим от Р. Например,

λ _0,68=1,0, λ _0,95=2,0, λ _0,997=3,0.

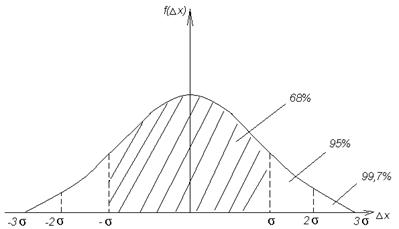
Рис. 1.1. Функция распределения для случайного отклонения

В теории вероятности показано, что можно оценить величину σ по отклонениям Δ x_i

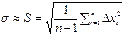, (1.7)

где S – средняя квадратичная погрешность отдельного наблюдения.

Среднее арифметическое совокупности результатов, безусловно, точнее характеризует значение измеренной величины, чем результат только одного наблюдения, поэтому стандартное отклонение среднего результата σ_n меньше σ. В теории вероятности показано, что 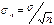, следовательно, средняя квадратичная погрешность окончательного результата опыта

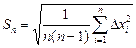, (1.8)

а полуширина доверительного интервала

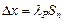. (1.9)

Чем больше число наблюдений n, тем точнее приближенное равенство (при 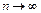σ = S), однако, практически нецелесообразно проводить большее число измерений для определения одной величины. В учебных лабораториях, как правило, n ~ 10. Это приводит к тому, что при заданной погрешности расширяется интервал Δ х, т.е. увеличивается множитель λ_P. Причем для различных n это увеличение будет различным. Таким образом, λ_P трансформируется в новый коэффициент t_n,p – коэффициент Стьюдента (табл. 1.1), причем, в пределе при n →∞; .

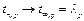Таблица 1.1

Коэффициенты Стьюдента

n	Pд =0,5	Pд =0,6	Pд =0,7	Pд =0,8	Pд =0,9	Pд =0,95	Pд =0,98	Pд =0,99
	1,00	1,38	1,96	3,08	6,31	12,71	31,82	63,66
	0,82	1,06	1,34	1,89	2,92	4,30	6,97	9,93
	0,77	0,98	1,25	1,64	2,35	3,18	4,54	5,84
	0,74	0,94	1,19	1,53	2,13	2,78	3,75	4,60
	0,73	0,92	1,16	1,48	2,02	2,62	3,37	4,03
	0,72	0,91	1,13	1,44	1,94	2,45	3,14	3,71
	0,71	0,90	1,12	1,42	1,90	2,37	3,00	3,50
	0,71	0,89	1,11	1,40	1,86	2,31	2,90	3,36
	0,70	0,88	1,10	1,38	1,83	2,26	2,82	3,25
	0,69	0,87	1,07	1,34	1,75	2,13	2,60	2,95
	0,69	0,86	1,06	1,32	1,71	2,06	2,49	2,80

С учетом коэффициента Стьюдента случайная погрешность результата, определяющая полуширину доверительного интервала около среднего значения измеряемой величины, может быть записана:

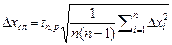(1.10)

Это основная формула для расчета случайных погрешностей прямых измерений.

ПРИМЕР. Пусть с помощью микроамперметра измеряется обратный ток через р-n переход. В результате измерений проявляются случайные ошибки, поэтому проведем десять (n =10) повторных наблюдений тока I (табл. 1.2).

Таблица 1.2

Обратный ток через p-n-переход

Номер наблюдения	Ii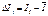, мкА	, мкА
	32,3	-0,22
	32,8	0,28
	32,4	-0,12
	32,7	0,18
	32,4	-0,12
	32,0	-0,52
	32,6	+0,08
	32,9	+0,38
	32,2	-0,32
	32,9	+0,38

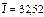
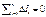
Определим результат и случайную погрешность измерения.

1. Найдем результат измерения – среднее арифметическое:

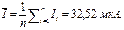
Промежуточные вычисления проводим с большей точностью (один знак), чем точность измерений, чтобы избежать заметных ошибок округления в окончательном ответе. Эта последняя цифра отбросится.

2. Определим случайные отклонения Δ Ι_i всех наблюдений от среднего значения (см. табл. 1.2).

3. Рассчитаем алгебраическую сумму Δ Ι_i. Если она не равна нулю, в вычислениях допущена ошибка, в нашем случае она равна нулю, т.е. расчеты правильны.

4. В шестом наблюдении значение I явно отличается от остальных значений. Его можно подозревать на промах. Для проверки рассчитаем среднюю квадратичную погрешность одного наблюдения.

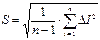=0,31 мкА.

5. Найдем предельную погрешность наблюдения – она в три раза больше чем S и составляет ΔΙ_пред =3 S =0,93 мкА.

6. Для промаха модуль отклонения превышает предельную погрешность 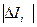> ΔΙ_пред. В данном случае 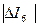= 0,52 мкА < ΔΙ_пред, следовательно промахи отсутствуют. Если бы они были обнаружены, то результаты таких измерений надо отбросить и расчеты провести заново. Если подозрений на промахи нет п.п. 4-6 можно пропустить.

7. Рассчитаем среднюю квадратичную погрешность измерения

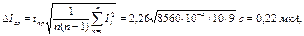
где коэффициент Студента t_{n , p} найден по таблице 1.1. Для числа наблюдений n =10 и доверительной вероятности P =0,95, t_{n , p} =2,26.

8. Определим относительную погрешность:

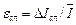=0,67% ≈ 0,7%,

таким образом, получим 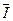=32,5 мкА;

ΔΙ_сл =0,2; 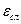= 0,7% при P = 0,95.