Из уравнения (25) следует, что х 2 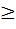 а2. Это означает, что в полосе между прямыми х = – а и х = + а нет ни одной точки гиперболы.
а2. Это означает, что в полосе между прямыми х = – а и х = + а нет ни одной точки гиперболы.
Точки, в которых гипербола пересекает действительную ось, называются её вершинами. Если действительная ось гиперболы совпадает с осью ОХ, то это будут точки (– а;0) и (+ а;0).
Поскольку в уравнение (25) переменные х и у входят во второй степени, то гипербола симметрична относительно координатных осей и, следовательно, достаточно изучить её форму в первой четверти, где она определяется уравнением
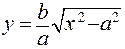 (27).
(27).
При х = а получаем у = 0. Найдём наклонную асимптоту гиперболы. Это прямая вида у = 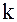
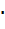 х + q. Здесь
х + q. Здесь
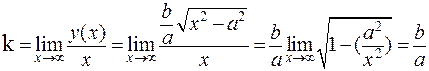 ,
,
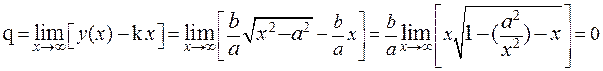
Таким образом, гипербола имеет две наклонные асимптоты
у = –  и у = +
и у = +  (28).
(28).
Для изображения гиперболы на чертеже сначала построим так называемый основной прямоугольник, центр которого совпадает с началом координат, а стороны равны 2 а и 2 b и параллельны соответственно координатным осям ОХ и ОУ. Прямые, сопадающие с диагоналями этого прямоугольника, и есть асимптоты гиперболы. Центр их пересечения называется центром гиперболы.
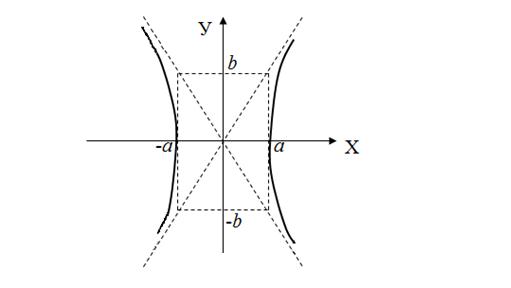
Рис. 4
Координатная ось, пересекающая гиперболу в двух точках, называется действительной осью, а другая координатная ось называется мнимой осью (она не имеет никаких общих точек с гиперболой). Отрезки [- а;+ а ] и [- b;+ b ] называются соответственно действительной и мнимой осями гиперболы, а отрезки [0;+ а ] и [0;+ b ] называются соответственно действительной и мнимой полуосями. Если а = b, то гипербола называется равносторонней. Её уравнение имеет вид
х 2 – у 2 = а2 (29).
В этом случае основной прямоугольник гиперболы становится квадратом со стороной 2 a.
Гипербола с действительной осью на координатной оси ОУ описывается уравнением
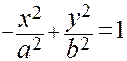 (30).
(30).
Если параллельным переносом центр гиперболы (25) переме-стить в (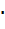 ) М0(х 0; у 0), то её уравнение примет вид
) М0(х 0; у 0), то её уравнение примет вид
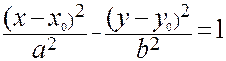 (31).
(31).
 2015-02-04
2015-02-04 959
959








