Пусть существуют 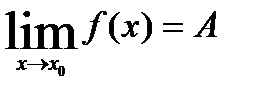 и
и 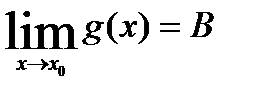
Теорема1: Постоянный множитель можно выносить за знак предела.
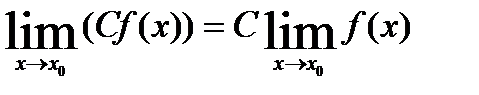 Пример:
Пример: 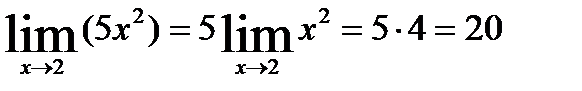
Теорема2: Предел суммы (разности) двух функций равен сумме (разности) их пределов.
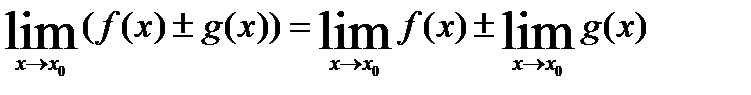 Пример:
Пример: 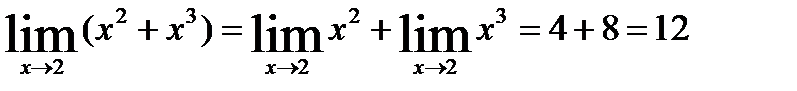
Теорема3: Предел произведения двух функций равен произведению их пределов.
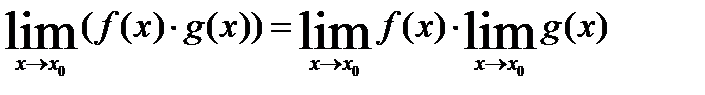 Пример:
Пример: 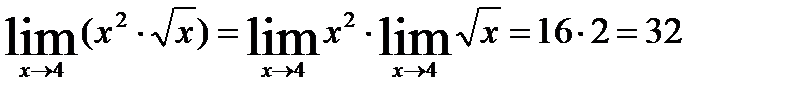
Теорема4: Предел дроби равен пределу числителя, деленному на предел знаменателя, если он не равен нулю. 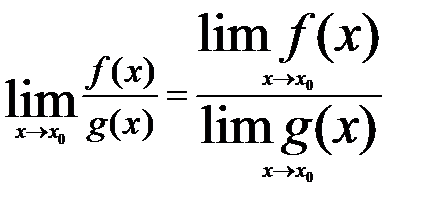
Теорема5: Предел степени с натуральным показателем равен той же степени предела.
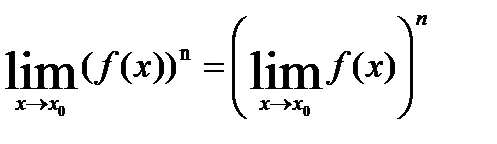 Пример:
Пример: 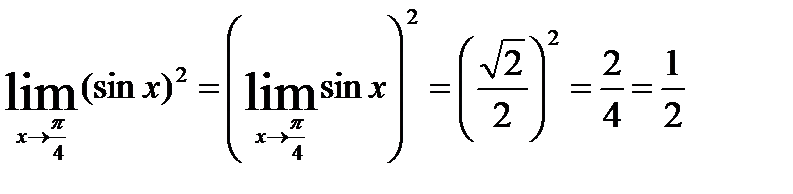
Теорема6 «Первый замечательный предел»:
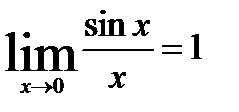 Пример:
Пример: 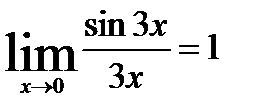
Теорема7 «Второй замечательный предел»:
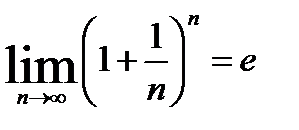 и
и 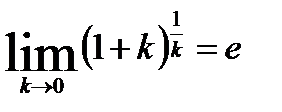
| А |
|
| Д |
| С |
| L |
| x0 |
| x0+∆x |
| ∆x=dx |
| df(x) |
| ∆f(x) |
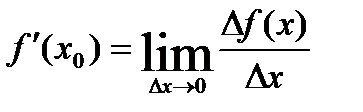 ,
,
tg α = f ’(x0) = k - геометрический смысл производной функции в точке.
Физический смысл производной функции в точке: производная от координаты по времени есть скорость: 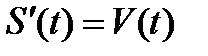 , производная от скорости по времени есть ускорение:
, производная от скорости по времени есть ускорение: 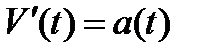
Таблица основных формул дифференцирования:
1. 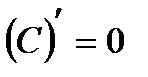 2.
2. 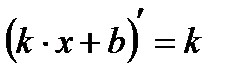 3.
3. 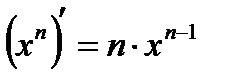 4.
4. 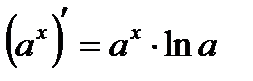 5.
5. 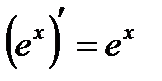 6.
6. 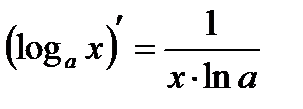 7.
7. 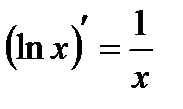 8.
8. 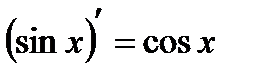 9.
9. 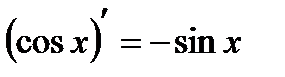 10.
10. 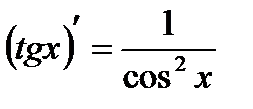 11
11 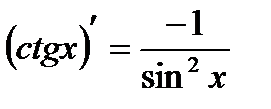
12. 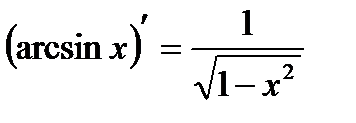 13.
13. 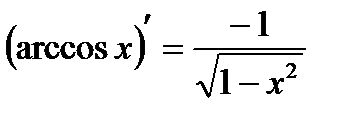 14.
14. 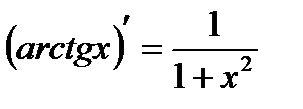 15.
15. 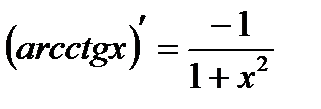
Правила дифференцирования:
1) 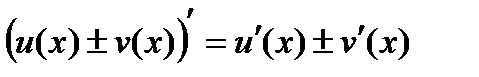 2)
2) 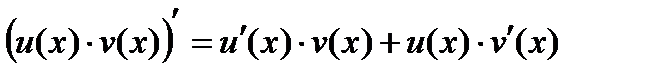
3) 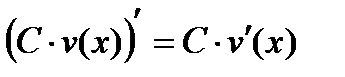 4)
4) 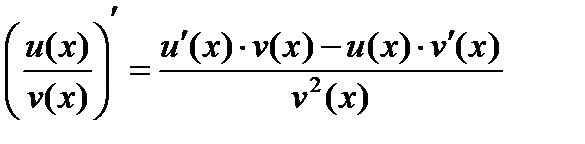
5) 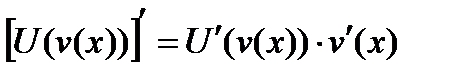
Производная высшего порядка: Второй производной функции y=f(x) называется: у" = (у')'. Третьей производной функции у=f(х) называется: у'" = (у")'.
Производной n-го порядка функции y=f(x) называется: у(п) = (уn-1)'.
Пусть задана функция z = f(x;y).
Если существует предел 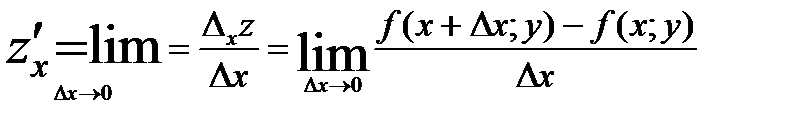 , то он называется частной производной функции z = f(x; у) в точке M(x;y) по переменной х и обозначается одним из символов:
, то он называется частной производной функции z = f(x; у) в точке M(x;y) по переменной х и обозначается одним из символов: 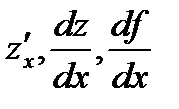
Частные производные по x в точке M0(x0;y0) обычно обозначают символами 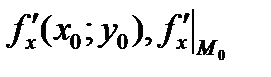
Аналогично определяется и обозначается частная производная от z = f(x; у) по переменной y
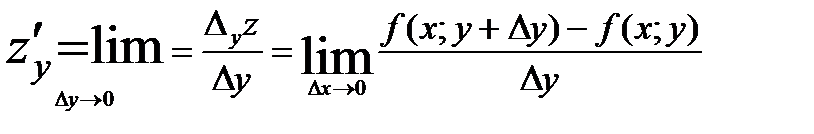
Частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции f(x;y) находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х или у считается постоянной величиной).
Пример 1. Найти частные производные функции 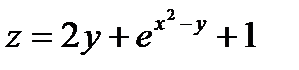
Решение:

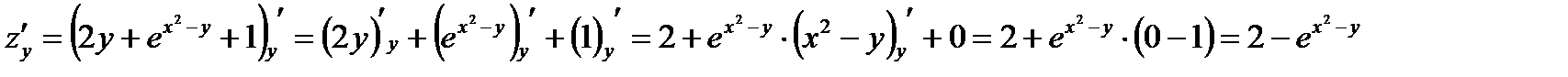
Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной.
Пример2. Найти смешанные частные производные второго порядка функции 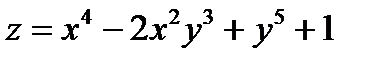
Решение: Так как 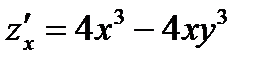 и
и 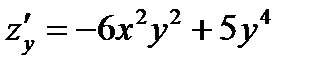 , то
, то
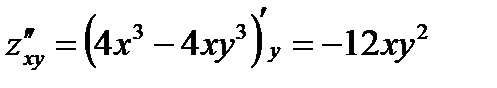 и
и 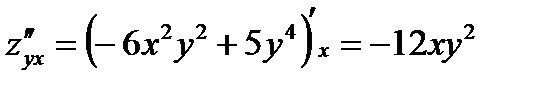
Полный дифференциал функции 1-го порядка: 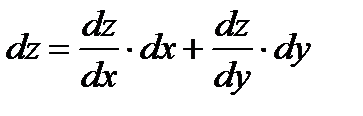
Полный дифференциал функции 2-го порядка определяется по формуле 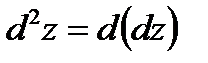 , т.е.
, т.е.
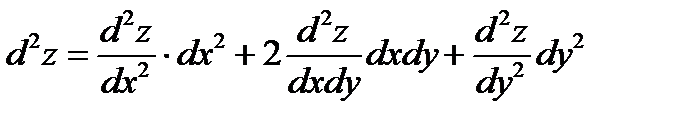
 2015-03-22
2015-03-22 537
537








