Метод хорд

Пусть дано уравнение f (x) = 0, где f (x) - непрерывная функция, имеющая в интервале (a, b) производные первого и второго порядков. Корень считается отделенным и находится на отрезке [ a, b ].

Идея метода хорд состоит в том, что на достаточно малом промежутке [ a, b ] дугу кривой y = f (x) можно заменить хордой и в качестве приближенного значения корня принять точку пересечения с осью абсцисс. Рассмотрим случай (рис. 1), когда первая и вторая производные имеют одинаковые знаки, т.е.
f '(x) f ²(x) > 0. Тогда уравнение хорды, проходящей через точки A ₀ и B, имеет вид

.

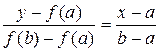Приближение корня x = x ₁, для которого y = 0, определяется как

.

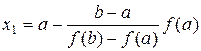Аналогично для хорды, проходящей через точки A ₁ и B, вычисляется следующее приближение корня

.

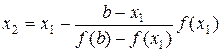В общем случае формула метода хорд имеет вид:

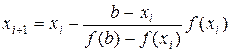. (2)

Если первая и вторая производные имеют разные знаки, т.е.

f '(x) f "(x) < 0,

то все приближения к корню x * выполняются со стороны правой границы отрезка [ a, b ], как это показано на рис. 2, и вычисляются по формуле:

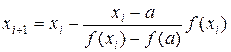. (3)

Выбор формулы в каждом конкретном случае зависит от вида функции f (x) и осуществляется по правилу: неподвижной является граница отрезка [ a, b ] изоляции корня, для которой знак функции совпадает со знаком второй производной. Формула (2) используется в том случае, когда f (b) f "(b) > 0. Если справедливо неравенство f (a) f "(a) > 0, то целесообразно применять формулу (3).

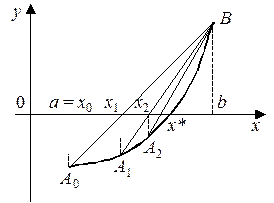
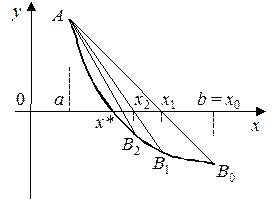
Рис. 1	Рис. 2
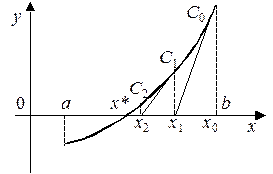
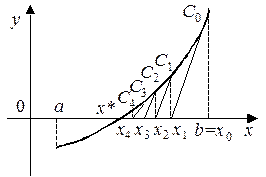
Рис. 3	Рис. 4

Итерационный процесс метода хорд продолжается до тех пор, пока не будет получен приближенный корень с заданной степенью точности. При оценке погрешности приближения можно пользоваться соотношением:

.

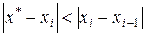Тогда условие завершения вычислений записывается в виде:

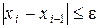, (4)

где e - заданная погрешность вычислений. Необходимо отметить, что при отыскании корня метод хорд нередко обеспечивает более быструю сходимость, чем метод половинного деления.