Следствия

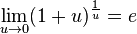
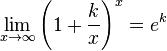
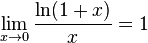
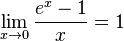
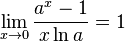для ,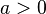

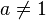
33. Непрерывные функции, их локальные и глобальные свойства. Теорема Вейерштрасса.

Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.

Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.

34. Производная вещественной функции одной вещественной переменной и ее геометрический смысл.

35. Уравнения касательной и нормали к графику Функции y=f(x).

Уравнения касательной и нормали

Уравнение касательной в декартовых координатах Предположим, что функция y = f (x) определена на интервале (a, b) и непрерывна в точке x 0 ∈ (a, b). В этой точке (точка M на рисунке 1) функция имеет значение y 0 = f (x 0). Пусть независимая переменная в точке x 0 получает приращение Δ x. Соответствующее приращение функции Δ y выражается формулой Δ y = f (x 0 + Δ x) − f (x 0). На рисунке 1 точка M 1 имеет координаты (x 0 + Δ x, y 0 + Δ y). Построим секущую MM 1. Ее уравнение имеет вид y − y 0 = k (x − x 0), где k − угловой коэффициент, зависящий от приращения Δ x и равный 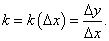При уменьшении Δ x точка M 1 стремится к точке M: M 1 → M. В пределе Δ x → 0 расстояние между точками M и M 1 стремится к нулю. Это следует из непрерывности функции f (x) в точке x 0: 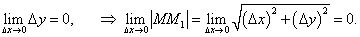Предельное положение секущей MM 1 как раз и представляет собой касательную прямую к графику функции y = f (x) в точке M. Возможны два вида касательных − наклонные и вертикальные.

36. Правила дифференцирования.

Дифференцирование – это вычисление производной.