2015-04-17
568
Метод аналогии является одним из методов человеческого мышления. Он заключается в перенесении знаний, полученных при наблюдении и оперировании с одними объектами или явлениями на другие объекты или явления. Источником аналогии является мир, в котором мы живём. Отражением этого свойства мира является мышление по аналогии, мышление метафорами. Уже ребёнок, говоря, что дерево так же высоко, как дом, мыслит по аналогии, метафорически. Мышление по аналогии – это обобщение, основанное на выявлении одинаковости каких – либо качеств, свойств объектов или явлений при кажущемся их различии. В этом смысле метод аналогии является одним из главных методов открытия общих законов природы. Данный метод является основой всех наук, в том числе и теории автоматического управления и математики, служащей задачам исследования АСР, и позволяет существенно упростить исследования.
Рассмотрим те положительные качества метода аналогии, которые повышают эффективность решения задач проектирования систем.
|
|
|
Возьмём в качестве примера простую механическую систему, состоящую из груза массой М, пружины с жесткостью С и демпфера, имеющего коэффициент демпфирования К, обусловленный вязкостью жидкости (рис.7.1).
Показанная система может представлять собой схематическое изображение весов или машины. Так для машины М – ее масса, С - жесткость рессор, К – коэффициент, характеризующий вязкость жидкости амортизаторов.
| F(t),н |
| y(t),см |
| в |
| б |
| а |
| Плавные процессы |
| Колебательные процессы |
| y(t) |
| МЕХАНИЧЕСКАЯ СИСТЕМА |
| К |
| С |
| F(t) |
t
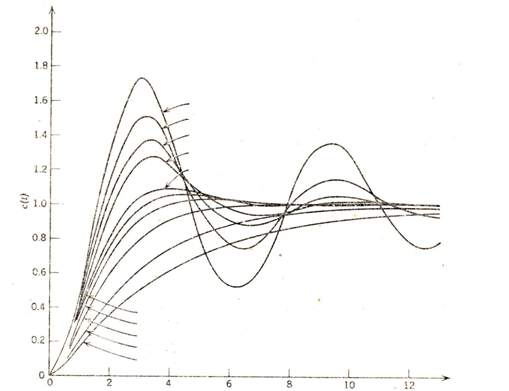
Рис.7.1. а) Система «масса-пружина-демпфер», б) блок- схема системы, в) процессы системы при разных параметрах М, К и С
Задача заключается в выборе таких значений К и С, при которых процесс взвешивания или процесс качания машины после наезда на преграду заканчивается за минимально короткое время и происходит плавно, без колебаний. Если первое требование понятно, то второе вытекает из желания уменьшить износ механических частей весов или машины и таким образом повысить надежность их работы, а для машины - сделать езду комфортной.
При решении задачи экспериментальным путём необходимо было бы изготовить различные пружины, взять разные по вязкости жидкости для демпферов. Задача выбора элементов в этом случае заключалась бы в использовании метода проб и ошибок, т.е. в изучении протекания процесса взвешивания при различных сочетаниях параметров М, К и С.
Математический (аналитический) метод исследования и выбора данных параметров системы начинается с получения модели системы, т.е. с получения её уравнения. Поскольку исследованию подлежит перемещение массы М во времени, следовательно, в качестве параметра, характеризующего состояние рабочего процесса (взвешивания), следует взять перемещение y(t). В качестве параметра состояния окружения принимаем силу F, действующую на систему. Таким образом, входным сигналом системы принимаем F (причина), а выходным – У (следствие). В соответствии с этим представлением рисуем блок – схему системы (рис.7.1.б).
|
|
|
Перед получением уравнения перемещения массы примем основные допущения, которые позволят абстрагироваться от несущественных сторон процесса.
Движение системы происходит в диапазоне упругих деформаций пружины, когда справедлив закон Гука.
Сопротивлением воздуха движению массы М по сравнению с сопротивлением жидкости демпфера пренебрегаем.
Трением поршня демпфера о его стенки пренебрегаем.
Правильность принятых предложений может быть установлена при дальнейшем сравнении результатов аналитического решения с практическими данными, полученными на реально выполненной системе. Если расхождение будет велико, то необходимо при проектировании выявить причину такого расхождения и учесть её при записи уравнения системы в дальнейших исследованиях.
Получим модель системы, пользуясь законом Ньютона (сила действия равна сумме сил противодействия). В результате будем иметь
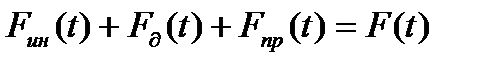(7.1)
Здесь Fин(t) – сила инерции массы М; Fд(t) - сила демпфирования; Fпр(t) – сила сопротивления пружины.
Раскроем смысл слагаемых, пользуясь известными законами:
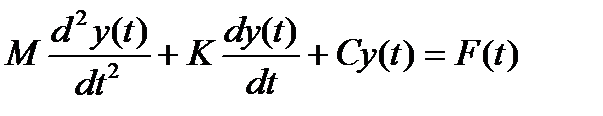. (7.2)
М, K и C – коэффициенты уравнения (7.2), т.е. параметры системы, характеризующие её собственные свойства (экстенсивные характеристики системы). Решение дифференциального уравнения (7.2) ищем как сумму двух решений – частного решения неоднородного уравнения (7.2) с правой частью и общего решения (7.2) без правой части. При таком подходе реализуется метод представления сложного через составляющие его простые части. Первое решение определяется характером действующей (вынуждающей) силы (УВ), а второе – собственными свойствами (параметрами) системы (УП):
У(t) = УВ(t) + УП(t). (7.3)
Здесь УВ(t) – вынужденная, а УП(t) – переходная составляющая решения У(t).
В данном случае при F(t)= Fo=const решение УВ(t) представляется в виде УВ(t)=УF=const. При постоянно действующей силе масса М с течением времени стремится к определенному положению УF, называемому установившимся значением У. Для нахождения УF=const подставим его в уравнение (7.2). Тогда получим
0 + 0 + СУF = F0,
откуда
УВ(t)=УF=F0 / С. (7.4)
Для нахождения УП(t) воспользуемся характеристическим уравнением системы
Mp2 + Kp + C = 0, (7.5)
найдём его корни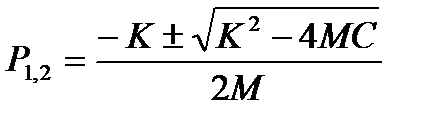 
(7.6)
и запишем решения УП(t) для случаев различных корней:
УП(t) =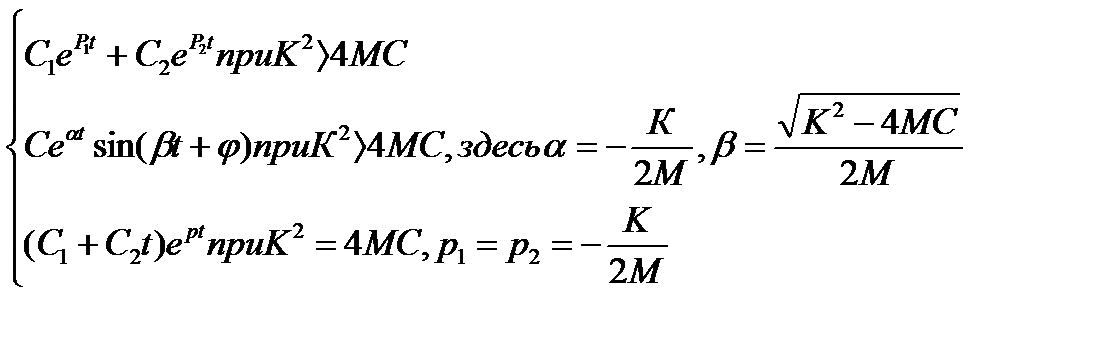 
(7.7)
Здесь С1,С2, С и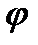 
- постоянные, которые находятся из начальных условий. Величины - 
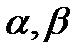- соответственно вещественная и мнимая части комплексных корней.
Полезно заметить, что характер изменения УП(t) определяется корнями характер истического уравнения (откуда и название уравнения). Данные корни в свою очередь связаны с коэффициентами характеристического и исходного дифференциального уравнений М, К и С, в которых находят отражение собственные свойства системы. Так как проектирование весов сводится к выбору М, К и С, то для получения требуемого вида У(t) необходимо оперировать с УП(t).
Рассмотрим решение задачи качественно. Из уравнения (7.6) следует, что движение весов без колебаний можно получить при условии К2>4mc и К2=4mc. Таким образом, если воспользоваться данными условиями при выборе М, K и C, задача будет существенно упрощена, так как число возможных переборов уменьшится за счет исключения случаев, когда
К2 < 4 МС.
Следующий этап заключается в количественном решении задачи. Для этого, подставляя в уравнение (7.5) различные значения М, К и С, путём, например, метода проб и ошибок, ищем такие их значения, при которых выполняются поставленные требования.
|
|
|
Рассмотрим другой пример RLC – цепи (рис.7.2). запишем уравнение динамики данной цепи (это уравнение можно получить на основе законов электротехники)
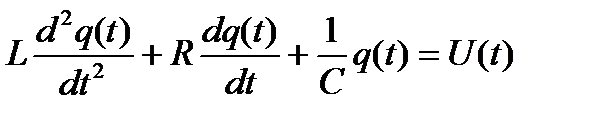(7.8)
Здесь L, R и С – соответственно значения индуктивности, сопротивления и ёмкости; q – количество электричества, U(t) – напряжение, подаваемое на цепь.
R L
| RLC- цепь |
U(t) C
Рис.7.2. RLC – цепь
Как и в предыдущем случае, имеем дифференциальное уравнение второго порядка с коэффициентами – параметрами цепи R, L и C. Для решения как уравнения (7.2), так и для уравнения (7.8), пользуемся сведениями решения дифференциального уравнения вида (7.9)
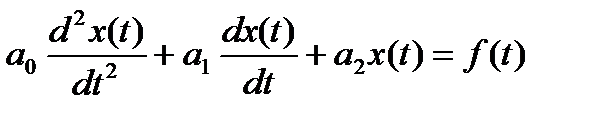, (7.9)
которые известны из математики.
Так, по образованному выражению А.Пуанкаре, «математика проявляет себя как искусство называть одним и тем же именем разные вещи».
Какое же отношение имеет это свойство аналогии, находящее отражение в математике, для решения задач теория автоматического управления?
При автоматизации приходится иметь дело с различными по физической природе объектами и процессами (механическими, гидравлическими, пневматическими, электрическими и т.д.). Аналогичность характера количественных изменений параметров состояний этих процессов находит отражение в математическом описании – моделях таких процессов, что позволяет воспользоваться теорией решения дифференциальных уравнений. Вместе с тем результаты, полученные в процессе разработки какой-либо одной системы, могут быть перенесены и на другую по физической природе систему.
В дальнейшем, пользуясь методом аналогии, существенно упростим вопросы проектирования АСР, сведя исследование множества различных по физической природе систем к исследованию одной абстрактной АСР, математическая модель которой представляет собой уравнение, имеющее в общем случае вид
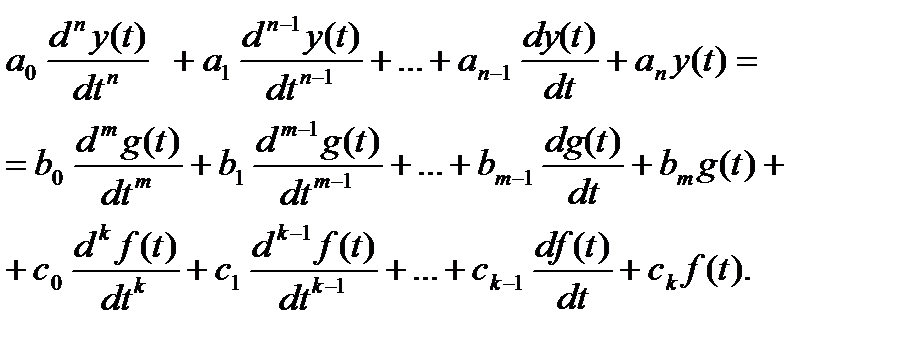(7.10)
Здесь y(t), f(t) и g(t) – соответственно регулируемая величина, возмущающее и задающее воздействия;
|
|
|
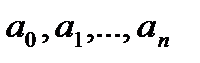– коэффициенты, характеризующие собственные свойства АСР;
; 
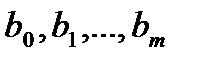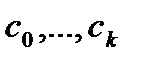– коэффициенты, связанные с воздействиями на систему.
Все результаты исследования данной модели по методу аналогии можно распространить на любую АСР, наполнив их конкретным физическим содержанием.
Таким образом, рассмотренный метод аналогии позволяет экономить мысль и время проектировщика систем, т.е. повысить производительность его труда.
Важно запомнить, что решение задач проектирования и расчета систем заключается в выборе элементов систем и их параметров, при которых достигается требуемое протекание процессов управления.
Выбор связан с выбором коэффициентов уравнений, описывающих процессы, а суждения о результатах такого выбора делаются на основе решения этих дифференциальных уравнений и получения решения в виде функции y(t), которая в каждом конкретном случае представляет собой или температуру жидкости или обороты двигателя или любую другую физическую величину, подлежащую регулированию.
Вопросы для самоконтроля
1.Что понимается под методом аналогии?
2. Что даёт сознательное применение метода аналогии при исследовании АСР?
3. В чём заключается качественное и количественное исследование математических моделей АСР?
