Сформулируем основные правила, которыми мы будем пользоваться при нахождении производных функций (дифференцировании).
1. 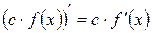 .
.
2. 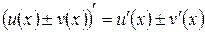 .
.
3. 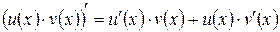 .
.
4. 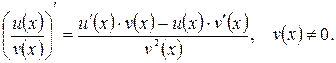
5. 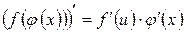 , где
, где 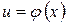 .
.
Докажем некоторые правила дифференцирования.
1. Вынесение постоянного множителя за знак производной.
g Если функция y = f (x) имеет в некоторой точке x производную
f ¢(x), то функция y = с × f (x), где с – постоянный множитель, также имеет в точке x производную, причем (с × f (x))¢ = f ¢(x).
4 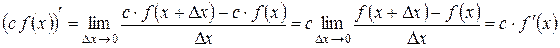 .3
.3
2. Производная суммы (разности) двух функций.
g Если функции y = u (x) и y = v (x) имеют в некоторой точке x производные u ¢(x) и v ¢(x) соответственно, то функция y = u (x) ± v (x) также имеет в точке x производную, причем (u (x) ± v (x))¢ = u ¢(x) ± v ¢(x).
4 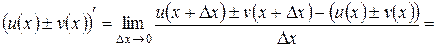
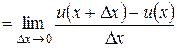
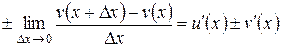 .3
.3
3. Производная произведения двух функций.
g Если функции y = u (x) и y = v (x) имеют в некоторой точке x производные u ¢(x) и v ¢(x) соответственно, то функция y = u (x)× v (x) также имеет в точке x производную, причем (u (x)× v (x))¢ = u ¢(x)× v (x) + v ¢(x)× u (x).
4 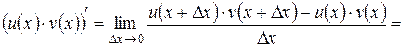
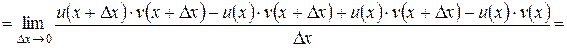
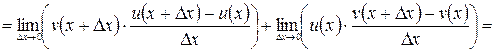
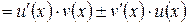 .3
.3
4. Аналогично выводится правило дифференцирования частного двух функций 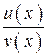 , имеющих производную в некоторой точке x
, имеющих производную в некоторой точке x 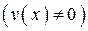 :
:
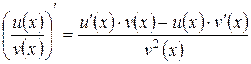 .
.
5. Производная сложной функции.
g Если 1) функция u = j (x) имеет в некоторой точке x производную
j ¢(x), 2) функция y = f (u) имеет в точке u = j (x) производную
f ¢(u), то сложная функция y = f (j (x)) будет иметь производную в точке x, равную произведению производной внешней функции f (u) на производную внутренней функции j (x). То есть 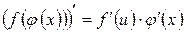 , где u = j (x).
, где u = j (x).
4 Обозначим через 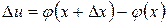 , тогда
, тогда
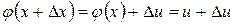 . В силу непрерывности функции u = j (x) приращение D u стремится к нулю при D x ® 0. Найдем производную
. В силу непрерывности функции u = j (x) приращение D u стремится к нулю при D x ® 0. Найдем производную
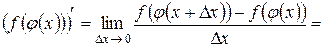
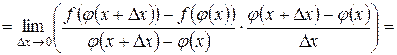
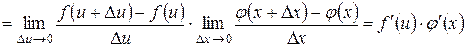 .3
.3
§5.5. Табличное дифференцирование.
Производная обратной функции
1. Табличное дифференцирование. В начале данного параграфа мы познакомимся с простейшими методами нахождения производных функций, основанными на таблице производных и правилах дифференцирования.
Сначала, используя правило дифференцирования частного двух функций, докажем еще две табличные формулы:
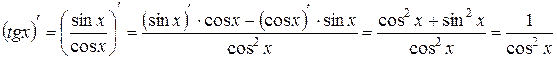 .
.
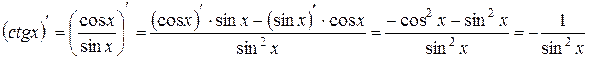 .
.
Пример 5.2. Найти производную функции 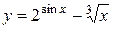 .
.
Воспользуемся правилом дифференцирования разности, учитывая, что вычитаемое является сложной функцией:
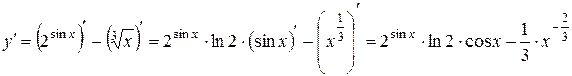 .
.
Задача 5.3. Найти производную функции 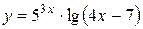 .
.
Решение. Воспользуемся правилом дифференцирования произведения двух функций, учитывая, что каждый сомножитель является сложной функцией:
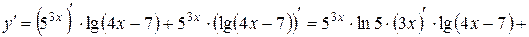
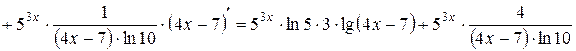 .
.
Задача 5.4. Найти производную функции 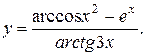
Решение. Воспользуемся правилом дифференцирования частного, учитывая при этом, что в числителе дроби стоит разность двух функций.
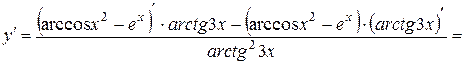
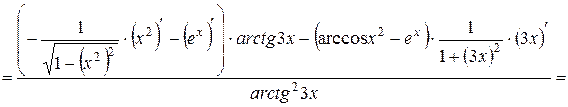
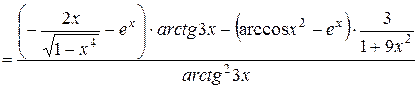 .
.
2. Производная обратной функции. g Пусть 1) функция y = f (x) имеет обратную функцию x = j (y) на интервале (a; b), 2) в точке x 0Î(a; b) имеет конечную и отличную от нуля производную f ¢ (x 0). Тогда обратная функция j (y) имеет производную в точке y 0 = f (x 0), причем 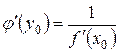 .
.
4Придадим значению y = y 0 произвольное приращение D y, тогда функция x = j (y) получит соответствующее приращение D x. Заметим, что при D y ¹ 0 ввиду однозначности функции y = f (x) и D x ¹ 0. Если D y ® 0 то и D x ® 0 в силу непрерывности функции x = j (y). Имеем
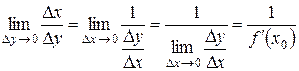 . 3
. 3
Мы доказали простую формулу для производной обратной функции:
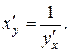 (5.8)
(5.8)
С помощью формулы (5.8) можно вывести оставшиеся табличные производные:
1. Найдем производную функции 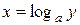 , являющейся обратной к функции
, являющейся обратной к функции 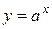 .
.
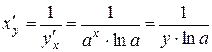 , то есть
, то есть 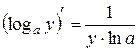 .
.
2. Найдем производную функции 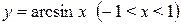 , являющейся обратной к функции
, являющейся обратной к функции 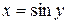 на интервале
на интервале 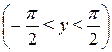 .
.
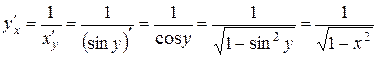 .
.
Мы доказали табличные формулы 3 и 8. Оставшиеся формулы
9 – 11 доказываются аналогично.
§5.6. Производная неявной функции и функции, заданной
параметрически. Логарифмическое дифференцирование
1. Производная неявной функции.
Предположим, что значения двух переменных x и y связаны между собой уравнением
F (x; y) = 0. (5.9)
Если для каждого значения x в некотором интервале существует одно или несколько значений y, которые совместно с x удовлетворяют уравнению (5.9), то этим определяется однозначная или многозначная функция y = f (x), для которой равенство F (x; f (x)) = 0 выполняется тождественно относительно x. Дифференцируя тождество (5.9) по переменной x, найдем производную неявной функции.
Пример 5.5. Найти производную y ¢(x) неявной функции:
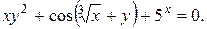
Продифференцируем данное равенство по переменной x. При этом производная x ¢ = 1 а производная y ¢ пока нам не известна. Ее мы как раз и найдем из полученного равенства:
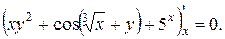
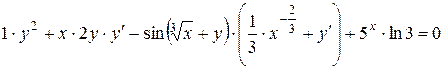 .
.
Раскроем скобки и сгруппируем слагаемые, содержащие в левой части равенства:
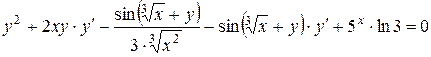 .
.
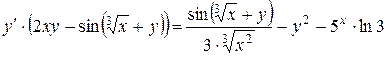 .
.
Из последнего равенства находим производную неявной функции
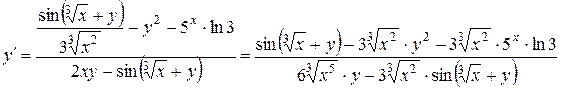 .
.
2. Производная функции, заданной параметрически.
Зависимость между переменными x и y может быть задана посредством некоторого параметра. Например, координаты точки на плоскости могут зависеть от времени. В общем случае параметрическое задание функции выглядит следующим образом
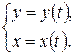 (5.10)
(5.10)
Если из системы удается исключить параметр t, то из параметрически заданной функции можно получить явную функцию y = f (x). Это возможно далеко не всегда, однако в любом случае мы можем найти производную y ¢(x). Для нахождения производной y ¢(x) мы воспользуемся формулой (5.6) из которой следует, что производная функции равна частному дифференциалов функции и независимой переменной: 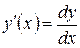 . Разделив числитель и знаменатель дроби на dt, получим:
. Разделив числитель и знаменатель дроби на dt, получим:
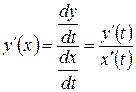 . (5.11)
. (5.11)
Замечание. Как видно из формулы (5.11) производная y ¢(x), так же как и переменные x и y зависит от параметра t. Поэтому производная функции, заданной параметрически снова является функцией, заданной параметрически:
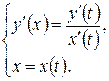
Пример 5.6. Найти производную y ¢(x) функции, заданной параметрически:
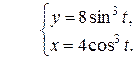
По формуле (5.11), получим
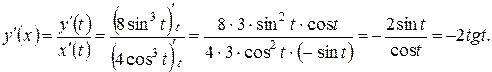
Следовательно, 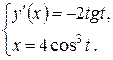
3. Логарифмическое дифференцирование.
Предположим, что требуется найти производную функции 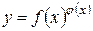 . Данную функцию нельзя дифференцировать, используя табличные формулы (1) и (2) (см. §5.2). Дело в том, что формула (1) предполагает постоянный показатель степени (степенная функция), а формула (2) – постоянное основание степени (показательная функция).
. Данную функцию нельзя дифференцировать, используя табличные формулы (1) и (2) (см. §5.2). Дело в том, что формула (1) предполагает постоянный показатель степени (степенная функция), а формула (2) – постоянное основание степени (показательная функция).
Прологарифмируем равенство 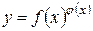 :
:
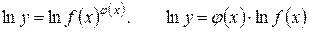 .
.
Вместо явной, мы получили неявную функцию. Однако правая часть полученного равенства является обычным произведением двух функций и, следовательно, легко дифференцируется:
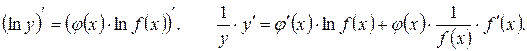
Из последнего равенства находим y ¢(x):
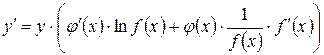 , или
, или
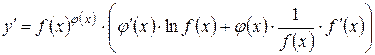 .
.
Пример 5.7. Найти производную функции 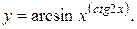
Логарифмируя данное равенство, получим неявную функцию:
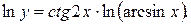
Дифференцируя, данное равенство по x, находим y ¢(x):
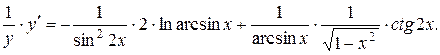
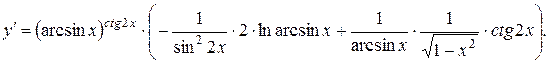
Логарифмическое дифференцирование наряду с дифференцированием показательно-степенных функций часто используется для нахождения производных функций, содержащих большое количество сомножителей.
Задача 5.8. Найти производную функции 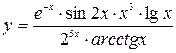 .
.
Решение. Прологарифмируем данное равенство:
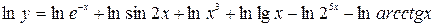 .
.
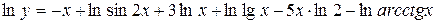 .
.
Дифференцируя, данное равенство по x, находим y ¢(x):
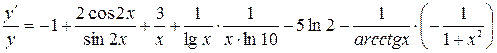 .
.
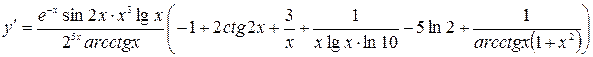 .
.
 2015-04-01
2015-04-01 2442
2442








