Решение задачи аналитическим методом осуществляется в математической среде MathCAD, где с помощью встроенных функций и команд имеется возможность решения дифференциальных уравнений. Зная основное ДУ теплопроводности, можно легко получить аналитическую зависимость изменения температуры и количества переданного тепла во времени для любой точки тела.
Сначала надо описать постоянные величины:
τ = 1000 – время расчета или нагрева пластины, с;
r = 0,1 – толщина пластины, м;
c – удельная массовая теплоемкость стали, 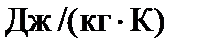 ;
;
ρ – плотность стали, кг/м3;
λ – коэффициент теплопроводности, 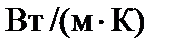 .
.
Для стали 20 средние для диапазона температур 0 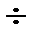 1473 0С теплофизические свойства представлены в таблице 3.1.
1473 0С теплофизические свойства представлены в таблице 3.1.
Таблица 3.1. Свойства материала
| Теплопроводность λ, Вт/(м·К) | Плотность ρ, кг/м3 | Теплоёмкость С, Дж/(кг·К) |
| 38.67 | 608.3 |
Затем записывается ДУ теплопроводности с начальными и граничными условиями, в виде указанном в постановке задачи. Записываются границы решения, и количество шагов по времени и по пространству, используя функцию pdesolve, которая как раз и является функцией решения дифференциальных уравнений в среде MathCAD.
|
|
|
Встроенная функция pdesolve применяется в рамках вычислительного блока, начинающегося ключевым словом Given, и пригодна для решения различных гиперболических и параболических уравнений. Она предназначена для решения одномерного уравнения (или системы уравнений) в частных производных (того, которое определит пользователь в рамках вычислительного блока Given), зависящего от времени t и пространственной координаты х, имеет целый набор различных аргументов и работает следующим образом: Pdesolve(u,x,xrange,t,trange,[xpts], [tpts]) – возвращает скалярную (для единственного исходного уравнения) или векторную (для системы уравнений) функцию двух аргументов (x, t), являющуюся решением дифференциального уравнения (или системы уравнений) в частных производных. Результирующая функция получается интерполяцией сеточной функции, вычисляемой согласно разностной схеме:
u – явно заданный вектор имен функций (без указания имен аргументов), подлежащих вычислению. Эти функции, а также граничные условия (в форме Дирихле или Неймана) должны быть определены пользователем перед применением функции pdesolve в вычислительном блоке после ключевого слова Given. Если решается не система уравнений в частных производных, а единственное уравнение, то, соответственно, вектор и должен содержать только одно имя функции и вырождается в скаляр;
х – пространственная координата (имя аргумента неизвестной функции);
xrange – пространственный интервал, т. е. вектор значений аргумента х для граничных условий. Этот вектор должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала);
|
|
|
t – время (имя аргумента неизвестной функции);
t range – расчетная временная область: вектор значений аргумента t, который должен состоять из двух действительных чисел (представляющих левую и правую границу расчетного интервала по времени);
xpts – количество пространственных точек дискретизации (может не указываться явно, в таком случае будет подобрано программой автоматически);
tpts – количество временных слоев, т. е. интервалов дискретизации по времени (также может не указываться пользователем явно).
Результаты решения приведены в табл. 3.2, а также получены в виде зависимостей, изображенных на рис. 3.1. Листинг программы в MathCAD приведен в приложении 2.
Таблица 3.2. Результаты решения задачи
| τ, сек | T(0, τ), оС |
| 430,83 | |
| 700,79 | |
| 889,09 | |
| 1015,56 | |
| 1100,37 |
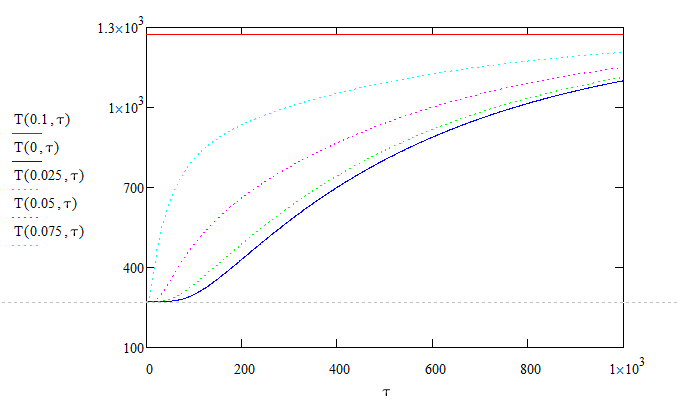
Рис. 3.1. График зависимости температур от времени нагрева
 2015-04-01
2015-04-01 1214
1214








