Пример 1. Вычислить работу, которую надо произвести, чтобы выкачать жидкость из заполненной ёмкости, имеющей форму полусферы радиуса 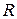 .
.
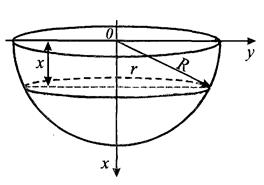 Направим ось
Направим ось 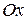 от центра поверхности жидкости вниз, тогда
от центра поверхности жидкости вниз, тогда 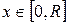 . На глубине
. На глубине 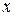 выделим слой жидкости толщиной
выделим слой жидкости толщиной 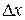 и будем приближенно считать его цилиндром. Радиус
и будем приближенно считать его цилиндром. Радиус 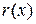 этого цилиндра найдём из соотношения
этого цилиндра найдём из соотношения
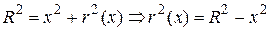 .
.
Элементарный объём выделенного слоя 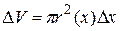 , масса слоя
, масса слоя 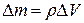 , где
, где 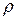 – плотность жидкости. Работа по поднятию
– плотность жидкости. Работа по поднятию 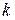 -го слоя на высоту
-го слоя на высоту 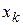 (элементарная работа) равна
(элементарная работа) равна 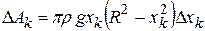 , а сумма таких работ
, а сумма таких работ 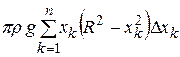 – это интегральная сумма для непрерывной функции
– это интегральная сумма для непрерывной функции 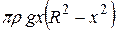 .
.
Значит, 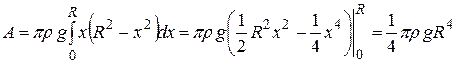 .
.
Пример 2. Вертикальная пластинка в форме треугольника с высотой 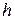 и основанием
и основанием 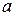 погружена в воду так, что её вершина лежит на поверхности. Найти силу давления воды на эту пластинку.
погружена в воду так, что её вершина лежит на поверхности. Найти силу давления воды на эту пластинку.
Направим ось 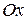 от поверхности воды вниз, тогда
от поверхности воды вниз, тогда 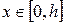 . На глубине
. На глубине 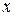 выделим элементарную полоску высотой
выделим элементарную полоску высотой 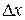 и будем приближенно считать её прямоугольной. Основание полоски
и будем приближенно считать её прямоугольной. Основание полоски 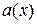 найдем из подобия треугольников:
найдем из подобия треугольников:
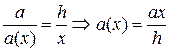 .
.
Значит, элементарная площадь равна 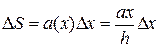 . По закону Паскаля выделенная полоска испытывает силу давления воды (одинаковую на данной глубине
. По закону Паскаля выделенная полоска испытывает силу давления воды (одинаковую на данной глубине 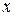 во всех направлениях)
во всех направлениях) 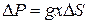 , а сумма
, а сумма 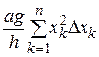 – это интегральная сумма для непрерывной функции
– это интегральная сумма для непрерывной функции 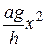 . Значит,
. Значит,  погруженная в воду пластинка испытывает давление
погруженная в воду пластинка испытывает давление
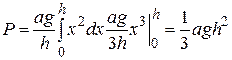 .
.
Пример 3. Определить массу стержня длины 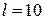 м, если линейная плотность стержня меняется по закону
м, если линейная плотность стержня меняется по закону 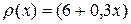 кг/м, где
кг/м, где 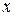 – расстояние от одного из концов стержня.
– расстояние от одного из концов стержня.
Выделим на расстоянии 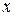 от одного из концов стержня участок длины
от одного из концов стержня участок длины 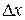 и будем приближенно считать, что плотность стержня вдоль этого участка не изменяется, т.е. остаётся такой же, как на его левом конце. Тогда элементарная масса (масса выделенного
и будем приближенно считать, что плотность стержня вдоль этого участка не изменяется, т.е. остаётся такой же, как на его левом конце. Тогда элементарная масса (масса выделенного 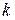 -го участка) равна
-го участка) равна 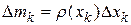 , а сумма таких масс
, а сумма таких масс 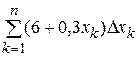 – это интегральная сумма для непрерывной функции
– это интегральная сумма для непрерывной функции 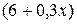 . Значит, масса стержня равна
. Значит, масса стержня равна 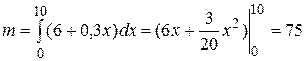 кг.
кг.
Пример 4. Вычислить скорость, которую необходимо сообщить телу, чтобы оно вышло из гравитационного поля Земли (вторая космическая скорость).
Найдем сначала величину работы, необходимой для поднятия тела массы 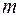 на высоту
на высоту 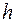 от поверхности Земли. Согласно закону всемирного тяготения величина силы
от поверхности Земли. Согласно закону всемирного тяготения величина силы 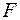 , с которой притягиваются два тела (материальные точки), определяется соотношением
, с которой притягиваются два тела (материальные точки), определяется соотношением 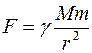 , в нашей задаче
, в нашей задаче 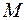 – масса Земли,
– масса Земли, 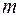 – масса тела,
– масса тела, 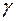 – гравитационная постоянная,
– гравитационная постоянная, 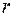 – расстояние между телом и центром Земли.
– расстояние между телом и центром Земли.
Как известно, работа 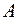 по перемещению в силовом поле, если перемещение
по перемещению в силовом поле, если перемещение 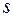 совпадает с направлением действия силы, вычисляется по формуле
совпадает с направлением действия силы, вычисляется по формуле 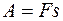 (при условии, что величина силы
(при условии, что величина силы 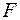 неизменна). Обозначим
неизменна). Обозначим 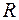 – радиус Земли, тогда расстояние между телом, поднятым на высоту
– радиус Земли, тогда расстояние между телом, поднятым на высоту 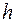 , и центром Земли изменяется в промежутке
, и центром Земли изменяется в промежутке 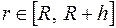 . Разобьем этот промежуток на части
. Разобьем этот промежуток на части 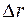 и будем полагать, что на каждом частичном промежутке сила изменяется незначительно, так что ее можно принять постоянной
и будем полагать, что на каждом частичном промежутке сила изменяется незначительно, так что ее можно принять постоянной 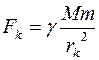 . При этом условии элементарная работа по поднятию тела на высоту
. При этом условии элементарная работа по поднятию тела на высоту 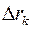 равна
равна 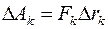 =
= 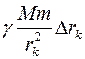 . Остается просуммировать все
. Остается просуммировать все 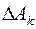 – получим интегральную сумму, а переход к пределу при
– получим интегральную сумму, а переход к пределу при 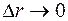 приводит к интегралу:
приводит к интегралу:
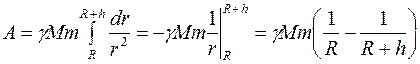 .
.
Устремив 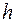 к бесконечности, получим величину работы, необходимой для того, чтобы тело навсегда покинуло Землю:
к бесконечности, получим величину работы, необходимой для того, чтобы тело навсегда покинуло Землю: 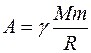 . Поскольку эта работа совершается за счет кинетической энергии тела:
. Поскольку эта работа совершается за счет кинетической энергии тела: 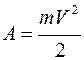 , то вторая космическая скорость равна
, то вторая космическая скорость равна 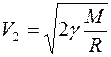 .
.
Пример 4. С какой силой притягивает материальная бесконечная прямая 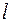 с постоянной линейной плотностью
с постоянной линейной плотностью 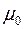 материальную точку
материальную точку 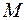 , находящуюся на расстоянии
, находящуюся на расстоянии 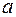 от этой прямой?
от этой прямой?
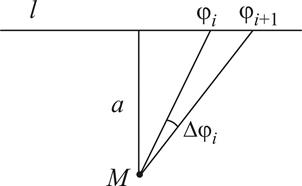
Введем полярную систему координат, поместив ее начало в материальную точку. Разобьем прямую на частичные отрезки так, что каждый из них можно считать материальной точкой и выделим один такой отрезок, концы которого во введенной системе координат соответствуют углам 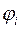 и
и 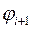 соответственно. Длина такого частичного отрезка
соответственно. Длина такого частичного отрезка 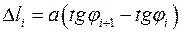 . Применяя формулу Лагранжа для функции
. Применяя формулу Лагранжа для функции 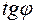 и учитывая малость частичного отрезка, можно считать, что его длина
и учитывая малость частичного отрезка, можно считать, что его длина 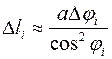 , а масса
, а масса 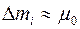
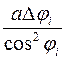 . Согласно закону всемирного тяготения, сила взаимного притяжения материальной точки
. Согласно закону всемирного тяготения, сила взаимного притяжения материальной точки 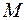 и массы
и массы 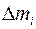 выделенного отрезка равна
выделенного отрезка равна 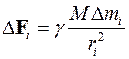 , где
, где 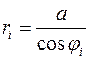 . Поэтому
. Поэтому
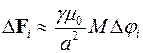
(здесь 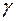 − гравитационная постоянная). Считаем массу
− гравитационная постоянная). Считаем массу 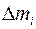 сосредоточенной в начальной точке отрезка
сосредоточенной в начальной точке отрезка 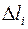 , сила
, сила 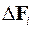 также приложена в этой точке. Заметим, что для каждого выделенного частичного отрезка найдется симметричный ему относительно точки пересечения полярной оси с материальной прямой. Разложим векторы силы притяжения материальной точки и двух таких частичных отрезков на два направления (вдоль и ортогонально к материальной прямой). Их результирующая вдоль прямой равна
также приложена в этой точке. Заметим, что для каждого выделенного частичного отрезка найдется симметричный ему относительно точки пересечения полярной оси с материальной прямой. Разложим векторы силы притяжения материальной точки и двух таких частичных отрезков на два направления (вдоль и ортогонально к материальной прямой). Их результирующая вдоль прямой равна 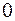 , а перпендикулярная к ней
, а перпендикулярная к ней
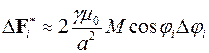 .
.
Для того чтобы найти полную силу 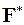 взаимного притяжения материальной точки
взаимного притяжения материальной точки 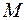 и бесконечной материальной прямой
и бесконечной материальной прямой 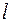 , необходимо просуммировать
, необходимо просуммировать 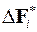 по всем таким парам симметричных частичных отрезков, а затем перейти к пределу при
по всем таким парам симметричных частичных отрезков, а затем перейти к пределу при 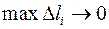 (
(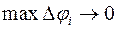 ). В результате получаем
). В результате получаем

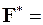
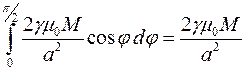 .
.
 2015-05-05
2015-05-05 1904
1904








