Две теоремы о гомоморфизмах

Тº. Пусть f – гомоморфизм группы G на 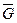и пусть Н – множество тех элементов группы G, которые при гомоморфизме f отображаются в элемент f (e), где е – единица группы G. Тогда Н нормальный делитель группы G.

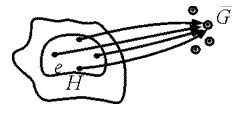◀ Достаточно доказать, что Н – подгруппа и, что левые смежные классы есть одновременно и правые смежные классы.

1) a Î H, b Î H Þ 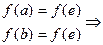f (ab) = f (a) f (b) =

= f (e) f (e) = f (ee) = f (e), т.е. ab Î H;

a Î H Þ f (a ^–1) = f (a ^–1 e) = f (a ^–1) f (e) = f (a ^–1) f (a) = f (a ^–1 a) = f (e), т.е. a ^–1Î H. Тогда Н – подгруппа группы G.

2) a Î G и пусть A = { x Î G ½ f (x) = f (a)}. Докажем, что А – это одновременно и левый и правый смежные классы.

Пусть a ¢Î A. Рассмотрим уравнение ax = a ¢: f (a ¢) = f (ax) = f (a)× f (x) = f (a ¢) f (x), отсюда f (x) = 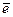= f (e) Þ x Î H; Т.к. 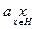= a ¢ Þ a ¢Î aH.

Пусть a ¢Î A. Рассмотрим уравнение xa = a ¢: f (a ¢) = f (xa) = f (x)× f (a) = f (x) f (a ¢)), отсюда f (x) = 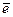= f (e) Þ x Î H; Т.к. 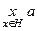= a ¢ Þ a ¢Î Ha.

Получили А = аН = На ▶

Тº. Пусть f – гомоморфизм группы G на 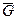и Н – тот нормальный делитель группы

G, элементaм которого при гомоморфизме f соответствует 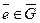. Тогда группа

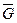и фактор-группа G / H изоморфны.

◀ Установим взаимно-однозначное соответствие между 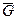и G / H.

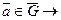смежный класс, который с помощью f отображается в .

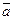Это отображение взаимно – однозначно, ибо смежные классы не пересекаются. Если умножение классов производить как умножение подмножеств, то станет ясно, что это ото-

бражение есть изоморфизм. Но классы смежности и есть элементы фактор-группы. ▶