Рассмотрим неоднородную линейную систему (2.2):
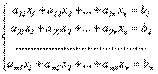 .
.
Докажем следующие свойства ее решений:
Свойство 1. Сумма любого решения системы (2.2) и любого решения соответствующей однородной системы (4.2) является решением системы (2.2).
Доказательство.
Пусть с1, с2,…,сn – решение системы (2.2), а d1, d2,…,dn – решение системы (4.2) с теми же коэффициентами при неизвестных. Подставим в систему (2.2) xi=ci+di:
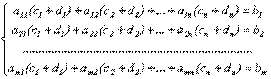 .
.
После перегруппировки слагаемых получим:
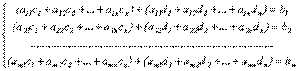 .
.
Но 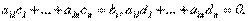 Следовательно, xi=ci+di является решением системы (2.2).
Следовательно, xi=ci+di является решением системы (2.2).
Свойство 2. Разность любых двух решений неоднородной системы (2.2) является решением соответствующей однородной системы (4.2).
Доказательство.
Пусть 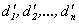 и
и 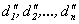 - решения системы (2.2). Тогда
- решения системы (2.2). Тогда
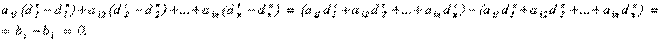 Утверждение доказано.
Утверждение доказано.
Следствие. Общее решение неоднородной системы (2.2) представляет собой сумму общего решения соответствующей однородной системы (4.2) и частного решения системы (2.2).
Пример.
Общее решение системы 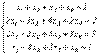 можно записать в виде:
можно записать в виде:
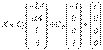 , где
, где 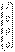 - частное решение данной системы.
- частное решение данной системы.
2.1.1. Пространство арифметических векторов R n. Линейные операции с векторами
Определение. Арифметическим вектором называется упорядоченная совокупность n чисел. Обозначается 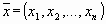 , числа
, числа 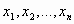 называются компонентами арифметического вектора.
называются компонентами арифметического вектора.
Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число: 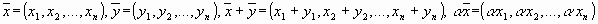 ,
,
для любых 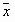 и
и 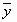 и любого числа
и любого числа 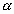
Определение. Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством рифметических векторов Rn.
Вектор 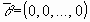 называется нулевым вектором, а вектор
называется нулевым вектором, а вектор 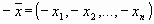 — противоположным вектором для вектора
— противоположным вектором для вектора 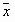 .
.
Для любых 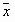 ,
, 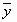 ,
, 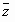 из Rn и любых чисел , справедливо:
из Rn и любых чисел , справедливо:
1. 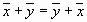 , сложение коммутативно;
, сложение коммутативно;
2. 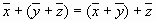 ,сложение ассоциативно;
,сложение ассоциативно;
3. 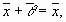
4. 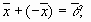
5. 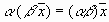 , умножение на число ассоциативно;
, умножение на число ассоциативно;
6. 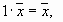 ;
;
7. 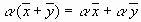 , умножение на число дистрибутивно относительно сложения элементов;
, умножение на число дистрибутивно относительно сложения элементов;
8. 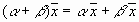 , умножение вектора на число дистрибутивно относительно сложения чисел.
, умножение вектора на число дистрибутивно относительно сложения чисел.
Примерами пространства арифметических векторов являются пространства геометрических векторов на плоскости, записанных в координатной форме.
2.1.2. Линейная зависимость и линейная независимость в R n
Говорят, что вектор 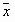 пространства Rn линейно выражается через векторы
пространства Rn линейно выражается через векторы 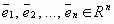 , если его можно представить в виде линейной комбинации этих элементов
, если его можно представить в виде линейной комбинации этих элементов 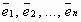 , т.е. представить в виде
, т.е. представить в виде 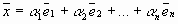 .
.
Определение. Если хотя бы один вектор системы векторов 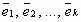 из Rn линейно выражается через остальные векторы системы, то система векторов называется линейно зависимой.
из Rn линейно выражается через остальные векторы системы, то система векторов называется линейно зависимой.
Определение. Система векторов, которая не является линейно зависимой, называется линейно независимой.
 2015-04-20
2015-04-20 552
552








