В табл. 1.1.1 приведены данные о зависимости объема продаж 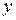 (тыс. шт.) от расходов на рекламу
(тыс. шт.) от расходов на рекламу 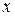 (усл. ед.) по 8 предприятиям концерна.
(усл. ед.) по 8 предприятиям концерна.
Таблица 1.1.1
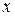
| 0,8 | 1,7 | 2,6 | 4,1 | 5,4 | 7,2 | ||
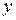
| 4,6 | 6,6 |
Полагая, что между 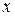 и
и 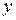 имеет место линейная зависимость, построить выборочное уравнение линейной регрессии.
имеет место линейная зависимость, построить выборочное уравнение линейной регрессии.
Решение. Коэффициенты регрессии 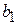 ,
, 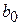 вычислим по формулам (1.1.17). Для удобства вычисления сумм оформим в виде табл. 1.1.2.
вычислим по формулам (1.1.17). Для удобства вычисления сумм оформим в виде табл. 1.1.2.
Таблица 1.1.2
| № п/п | x | y | xy | 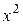
| 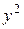
| |
| 0,8 | 5,6 | 4,48 | 0,64 | 31,36 | ||
| 6,6 | 6,6 | 43,56 | ||||
| 1,7 | 20,4 | 2,89 | ||||
| 2,6 | 6,76 | |||||
| 4,1 | 86,1 | 16,81 | ||||
| 5,4 | 29,16 | |||||
| 7,2 | 172,8 | 51,84 | ||||
| Сумма | 30,8 | 135,2 | 672,38 | 173,1 | 18279,04 | |
| Среднее | 3,85 | 16,9 | 84,0475 | 21,637 | 285,61 |
В результате получим
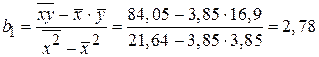 ,
, 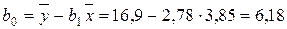 .
.
Таким образом, уравнение парной линейной регрессии имеет вид 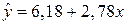 .
.
Полученные значения коэффициентов легко проверить с помощью стандартных статистических функций MS Excel НАКЛОН(Y;X) и ОТРЕЗОК(Y;X) соответственно.
Величина 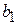 показывает, что с увеличением расходов на рекламу на 1 усл. ед. объем продаж предприятия возрастает в среднем на 2,78 тыс. шт. Величина
показывает, что с увеличением расходов на рекламу на 1 усл. ед. объем продаж предприятия возрастает в среднем на 2,78 тыс. шт. Величина 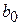 имеет значение объема продаж предприятия в случае отсутствия рекламы.
имеет значение объема продаж предприятия в случае отсутствия рекламы.
Статистические свойства МНК-оценок
Рассмотрим вопросы качества и точности полученных оценок.
Найденные по МНК коэффициенты являются лишь выборочными точечными оценками истинных параметров регрессии. Выборочные оценки 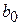 и
и 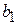 являются случайными величинами, так как зависят от выборки
являются случайными величинами, так как зависят от выборки 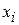 и
и 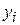 , а также от метода расчета. Критериями качества точечных оценок в статистике являются такие их свойства, как несмещенность, состоятельность и эффективность.
, а также от метода расчета. Критериями качества точечных оценок в статистике являются такие их свойства, как несмещенность, состоятельность и эффективность.
Учитывая, что 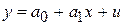 , и воспользовавшись разложением
, и воспользовавшись разложением
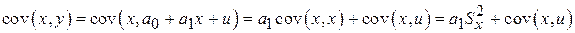 ,
,
выражения (1.1.14) для 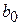 и
и 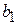 можно представить в эквивалентном виде
можно представить в эквивалентном виде
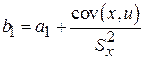 ;
; 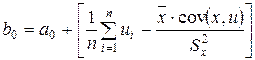 . (1.1.19)
. (1.1.19)
Таким образом, выборочные коэффициенты регрессии представлены в виде суммы постоянной составляющей (истинного значения) и случайной составляющей, зависящей от случайного отклонения модели 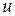 , а значит, и от свойств
, а значит, и от свойств 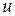 .
.
Из (1.1.19) находятся статистические характеристики коэффициентов 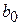 и
и 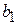 .
.
Математические ожидания:
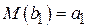 ,
, 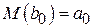 . (1.1.20)
. (1.1.20)
Дисперсии:
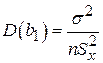 ,
, 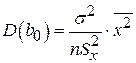 . (1.1.21)
. (1.1.21)
Ковариационная матрица:
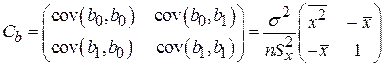 . (1.1.22)
. (1.1.22)
Из выражений (1.1.20)-(1.1.22) следует, что оценки параметров 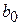 и
и 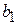 являются несмещенными (математическое ожидание оценки равно истинному значению) и состоятельными. Действительно, оценка состоятельна, если сходится по вероятности к истинному значению параметра. Для несмещенных оценок достаточным условием сходимости является сходимость их дисперсии к нулю при неограниченном возрастании объема выборки. Справедлива также теорема Гаусса-Маркова.
являются несмещенными (математическое ожидание оценки равно истинному значению) и состоятельными. Действительно, оценка состоятельна, если сходится по вероятности к истинному значению параметра. Для несмещенных оценок достаточным условием сходимости является сходимость их дисперсии к нулю при неограниченном возрастании объема выборки. Справедлива также теорема Гаусса-Маркова.
Теорема Гаусса-Маркова. Если регрессионная модель (1.1.3) удовлетворяет условиям (1.1.5)-(1.1.8), то МНК-оценки имеют наименьшую дисперсию в классе всех линейных несмещенных оценок (являются эффективными оценками).
Несмещенной оценкой дисперсии возмущений 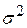 является величина
является величина
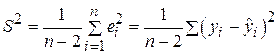 , (1.1.23)
, (1.1.23)
которая служит мерой разброса зависимой переменной и называется остаточной дисперсией. Величина S называется стандартной ошибкой регрессии.
Несмещенные оценки дисперсий коэффициентов 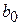 и
и 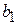 получаются путем замены в (1.1.21) неизвестного значения дисперсии возмущения
получаются путем замены в (1.1.21) неизвестного значения дисперсии возмущения 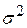 его оценкой (1.1.23):
его оценкой (1.1.23):
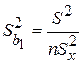 ,
, 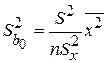 . (1.1.24)
. (1.1.24)
Величины 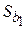 и
и 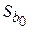 – стандартные отклонения (ошибки) МНК-коэффициентов регрессии.
– стандартные отклонения (ошибки) МНК-коэффициентов регрессии.
После этапа оценивания модели следует этап проверки ее качества, который включает:
· проверку статистической значимости оценок параметров регрессии;
· построение доверительных интервалов параметров регрессии, дающих определенные гарантии точности их оценок;
· проверку общего качества уравнения регрессии;
· проверку качества прогнозов результативного признака.
Пример 1.1.2
Для данных примера 1.1.1 рассчитать стандартную ошибку регрессии и стандартные ошибки коэффициентов регрессии.
Решение. Подставляя рассчитанные в примере 1.1.1 значения 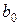 и
и 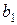 в формулу
в формулу 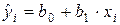 , найдем значения
, найдем значения 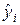 и разместим их в седьмом столбце табл. 1.1.3. Таблица 1.1.3
и разместим их в седьмом столбце табл. 1.1.3. Таблица 1.1.3
| № п/п | 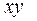
| 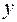
| 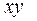
| 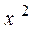
| 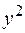
| 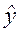
| 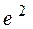
| 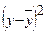
| |
| 0,8 | 5,6 | 4,48 | 0,64 | 31,36 | 8,404 | 7,8624 | 127,69 | ||
| 6,6 | 6,6 | 43,56 | 8,96 | 5,5696 | 106,09 | ||||
| 1,7 | 20,4 | 2,89 | 10,906 | 1,1968 | 24,01 | ||||
| 2,6 | 6,76 | 13,408 | 2,5345 | 3,61 | |||||
| 4,1 | 86,1 | 16,81 | 17,578 | 11,71 | 16,81 | ||||
| 5,4 | 29,16 | 21,192 | 14,501 | 65,61 | |||||
| 7,2 | 172,8 | 51,84 | 26,196 | 4,8224 | 50,41 | ||||
| 28,42 | 5,8564 | 82,81 | |||||||
| Сумма | 30,8 | 135,2 | 672,38 | 173,1 | 2761,92 | 54,053 | 477,04 | ||
| Среднее | 3,85 | 16,9 | 84,0475 | 21,6375 | 345,24 |
В восьмом столбце таблицы рассчитаем значения 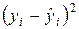 . Вычислив соответствующие суммы, найдем несмещенную оценку дисперсии ошибки
. Вычислив соответствующие суммы, найдем несмещенную оценку дисперсии ошибки 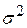 по формуле (1.1.23) и оценки дисперсий коэффициентов регрессии по формулам (1.1.24):
по формуле (1.1.23) и оценки дисперсий коэффициентов регрессии по формулам (1.1.24):
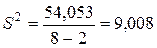 ,
, 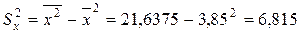 ,
, 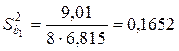 ,
, 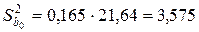 .
.
Значения соответствующих стандартных ошибок 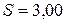 ,
, 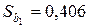 ,
, 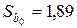 .
.
Вопросы для самопроверки
1. Какая зависимость называется статистической?
2. Какая связь между переменными называется корреляционной?
3. Какая функция называется функцией регрессии?
4. Чем отличаются парная и множественная регрессионные модели?
5. Перечислите этапы построения модели регрессии.
6. Как выглядит линейная модель парной регрессии?
7. Каковы предпосылки классической регрессионной модели?
8. Назовите основные причины наличия в регрессионной модели случайного отклонения.
9. В чем суть метода наименьших квадратов (МНК) и для чего он используется?
10. Приведите формулы расчета оценок коэффициентов линейной модели по МНК.
11. Дайте содержательную интерпретацию коэффициента регрессии в линейном парном уравнении регрессии?
12. Какими свойствами обладают МНК-оценки классической линейной эконометрической модели?
13. Как оценивается дисперсия истинной ошибки модели?
 2015-05-18
2015-05-18 926
926








