Уравнение Р(х;у)·dx + Q(х;у)·dу = 0 (12) - уравнение в полных дифференциалах, если его левая часть есть полный дифференциал функции U(х;у) т.е. Р(х;у)·dx + Q(х;у)·dу = du(х;у).
В этом случае ДУ (12) можно записать в виде du(х;у) = 0,
а его общий интеграл будет: U(х;у) = с. (13)
Δ = Р(х;у)·dx + Q(х;у) – полный дифференциал, если Р(х;у) и Q(х;у) - функции и 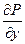 и
и 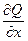 их частные производные, то
их частные производные, то 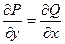 (14).
(14).
Функция U(х, у) может быть найдена из системы уравнений:
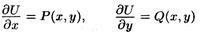 или по формуле:
или по формуле:
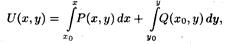
где (хо, уо) некоторая фиксированная точка из области непрерывностифункций Р(х, у), Q(х, у) и их частных производных.
Пример 5. Решить уравнение 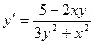
Решение: Запишем уравнение в дифференциальной форме:
(2ху–5)·dx+ (3у2+х2)·dy=0
Здесь Р(х;у) = 2ху – 5, Q(х;у) = 3у2 + х2. Проверяем выполнение условия (14):
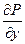 =2х;
=2х; 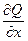 =2х;
=2х; 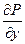 =
= 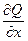
Следовательно, данное уравнение есть уравнение в полных дифференциалах.
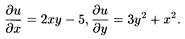
Отсюда имеем du(х;у). = ∫ (2ху–5)·dx = х2у–5х+φ(у);
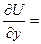 (х2у–5х+φ(у))′у= х2+φ′(у). 3у2+х2 = х2+φ′(у), φ′(у) = 3у2,φ(у) = у3 + с1, du(х;у) = х2у–5х + у3+с1. Общим интегралом является х2у–5х + у3 + с1=с2, или х2у–5х + у3 = с, где с = с2 – с1.
(х2у–5х+φ(у))′у= х2+φ′(у). 3у2+х2 = х2+φ′(у), φ′(у) = 3у2,φ(у) = у3 + с1, du(х;у) = х2у–5х + у3+с1. Общим интегралом является х2у–5х + у3 + с1=с2, или х2у–5х + у3 = с, где с = с2 – с1.
|
|
|
Замечание. Если условие (14) не выполняется для уравнения (12), то в ряде случаев его можно свести к уравнению в полных дифференциалах умножением на некоторую функцию t(х, у) = t, - интегрирующий множитель, который. находится в двух случаях: если t = t(х) или t = t(у);
в первом случае 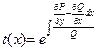 , зависящее только от х.
, зависящее только от х.
во втором 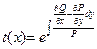 ,зависящее только от у.
,зависящее только от у.
Пример. Решить уравнение (х2 – у) ·dх + (х2у2 + х) ·dу = 0.
Решение. Здесь 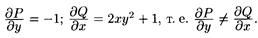
Однако 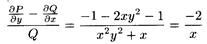 зависит от х.
зависит от х.
Следовательно, уравнение имеет интегрирующий множитель, зависящий только от х, выражение которого может быть получено при помощи формулы (24). В нашем случае получим, что
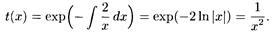
Умножая исходное уравнение на 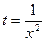 , получаем
, получаем 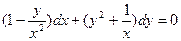
т. е. уравнение в полных дифференциалах! Решив его, найдем, что общий интеграл заданного уравнения имеет вид 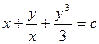 .
.
 2015-05-20
2015-05-20 426
426








