Рассмотрим наиболее распространенные методы получения последовательности квазиравномерных случайных чисел с помощью ЭВМ.
Методы получения последовательностей квазиравномерных псевдослучайных чисел. Рассмотрим простейшие приёмы получения на ЭВМ последовательностей квазиравномерных ПСЧ на отрезке [0,1].
Метод Неймана (середины квадратов). Пусть имеется n -разрядное число x 0, принадлежащее отрезку [0,1]. Это число возводится в квадрат, т.е. получается 2 n -разрядное число 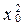 . В нем выделяются средние n разрядов, слева к которым приписывается 0. Таким образом, получается очередное число последовательности квазиравномерных ПСЧ x 1, которое затем возводится в квадрат и так далее.
. В нем выделяются средние n разрядов, слева к которым приписывается 0. Таким образом, получается очередное число последовательности квазиравномерных ПСЧ x 1, которое затем возводится в квадрат и так далее.
Пример. Пусть 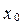 = 0,0713, тогда
= 0,0713, тогда 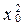 = 0,00508369. Отбрасывая крайние два символа (после запятой и в самом конце), получаем x 1= 0,5083. Аналогично получаем x 2 = 0.8368 и т.д..
= 0,00508369. Отбрасывая крайние два символа (после запятой и в самом конце), получаем x 1= 0,5083. Аналогично получаем x 2 = 0.8368 и т.д..
Мультипликационный метод. Получение последовательностей квазиравномерных ПСЧ по этому методу происходит на основе рекуррентного соотношения
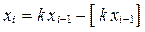 ,
,
где 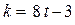 ; t – целое положительное число; операция
; t – целое положительное число; операция 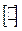 означает взятие целой части числа.
означает взятие целой части числа.
|
|
|
Пример. Пусть x 0 = 0,37843, t = 5, 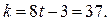 Тогда x 1= k x 0 − [ k x 0] = = 0,00191 – второе число последовательности квазиравномерных ПСЧ.
Тогда x 1= k x 0 − [ k x 0] = = 0,00191 – второе число последовательности квазиравномерных ПСЧ.
Метод произведений. Пусть имеется два числа x 0 и x 1, у которых число знаков после запятой одинаково и равно n.
В результате перемножения этих чисел получается число 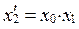 . После выделения из
. После выделения из 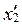 n средних цифр и приписывания слева нуля имеем число x 2 < 1. Последующее числа получаются аналогичным образом.
n средних цифр и приписывания слева нуля имеем число x 2 < 1. Последующее числа получаются аналогичным образом.
Мультипликативный конгруэнтный метод (метод вычетов). Полученные, с помощью идеального генератора, последовательности чисел должны состоять:
- из равномерно распределённых чисел;
- из статистически независимых чисел;
- из воспроизводимых чисел;
- из неповторяющихся чисел.
Кроме того генератор чисел должен работать быстро и занимать минимальный объём памяти ЭВМ.
Всей совокупности перечисленных выше требований лучше, чем другие методы генерирования случайных чисел, удовлетворяют так называемые конгруэнтные методы, к числу которых относится и метод вычетов.
В методе вычетов используется соотношение
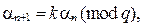
где запись 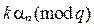 означает остаток от деления
означает остаток от деления 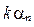 на
на 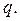
При этом 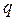 представляется в виде q = 10 d. Выбирая соответствующим образом
представляется в виде q = 10 d. Выбирая соответствующим образом 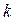 и
и 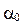 , можно получить хорошее качество последовательностей квазиравномерных ПСЧ, распределенных на отрезке [0,1].
, можно получить хорошее качество последовательностей квазиравномерных ПСЧ, распределенных на отрезке [0,1].
Пример. Для получения хорошего качества последовательностей квазиравномерных ПСЧ рекомендуется брать α0 = 3141592, q = 10 d, d = 8, k = 200 t ± p. Здесь t – любое целое число, p – берется из набора чисел 3, 11, 13, 19, 21, 27, 29, 37, 53, 59, 61, 67, 69, 77, 83 и 91.
Пусть t = 0, p = 91. Тогда k = ± 91. Положим k = 91.
|
|
|
В этом случае 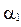 будет равно остатку от деления
будет равно остатку от деления
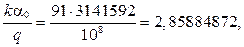
т.е. 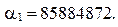
Поставив запятую слева от найденного числа 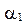 , будем иметь первое число последовательности
, будем иметь первое число последовательности 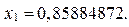
Аналогично 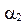 будет равно остатку от деления
будет равно остатку от деления
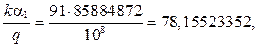
т.е. 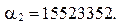
Поставив запятую слева от 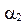 , получим второе число последовательности
, получим второе число последовательности 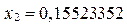 и т.д.
и т.д.
Максимальный период повторения чисел равен 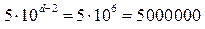 .
.
Метод Лемера. Получение последовательности квазиравномерных ПСЧ этим методом осуществляется на основании того же соотношения, что и в методе вычетов, но q равно не 10 d, а 2 d, т.е. метод Лемера предназначен для работы в двоичной системе счисления.
В этом случае максимальный период повторения чисел равен 2 d −2.
Проверка качества последовательностей квазиравномерных псевдослучайных чисел. Качество и эффективность машинной имитации существенным образом зависят от того, насколько удачно выбран вид рекуррентного соотношения 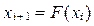 , для получения ПСЧ. Так как это соотношение выбирается эмпирически, то необходимо убедиться, что ПСЧ последовательности принадлежат отрезку [0, 1] и удовлетворяют требованиям стохастичности и равномерности. Для этого обычно используются:
, для получения ПСЧ. Так как это соотношение выбирается эмпирически, то необходимо убедиться, что ПСЧ последовательности принадлежат отрезку [0, 1] и удовлетворяют требованиям стохастичности и равномерности. Для этого обычно используются:
1. Проверка по моментам распределения полученных чисел. Если генерируемые ПСЧ близки к случайным числам, равномерно распределенным на отрезке [0,1], то оценки их математического ожидания 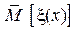 и дисперсии
и дисперсии 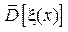
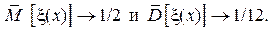
2. Проверка на равномерность полученных чисел по гистограмме. Отрезок [0, 1] разбивается на m равных частей (интервалов). При генерации каждое из чисел 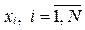 с вероятностью
с вероятностью 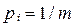 попадёт в один из этих интервалов.
попадёт в один из этих интервалов.
Всего в каждый j - й интервал попадёт Nj чисел последовательности, 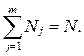 Относительная частота попадания случайных чисел в каждый из интервалов
Относительная частота попадания случайных чисел в каждый из интервалов 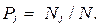
Необходимо построить гистограмму Pi = f (xi). Если случайные числа xi принадлежат последовательности квазиравномерных ПСЧ, то при достаточно больших N гистограмма должна приближаться к теоретической прямой 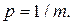 Обычно полагают
Обычно полагают 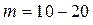 , а
, а 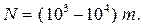
 2015-05-20
2015-05-20 2237
2237








