Анализ плоского напряженного состояния

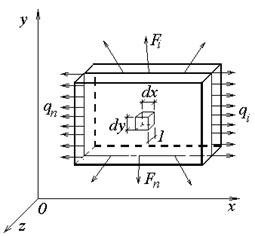
Пластина под действием нагрузки, приложенной в ее серединной плоскости, параллельной координатной плоскости х0у, находится в состоянии равновесия. Выделим плоскостями, параллельными координатным плоскостям, элементарный параллелепипед с размерами dх, dу и 1 (рис.3.6).

Рис.3.6 Рис.3.7

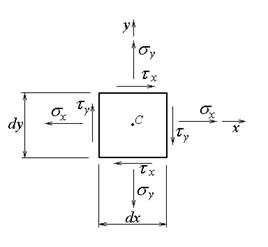
Согласно методу сечений, усилия взаимодействия элемента с телом представим напряжениями s и τ. Очевидно, что на гранях, параллельных координатной плоскости х0у, напряжения будут отсутствовать. Также будут отсутствовать на остальных 4 гранях составляющие касательных напряжений в направлении оси z. Элемент, таким образом, будет находиться в плоском напряженном состоянии. Изобразим его в прямой проекции (рис.3.7). При этом по каждой из 4 граней, перпендикулярных плоскости х0у, будут действовать нормальное и одно касательное напряжения. Обозначим их нижними индексами, в качестве которых используем наименования координатных осей, параллельно которым действуют рассматриваемые напряжения (рис.3.7).

Используем для напряжений следующее правило знаков:

нормальные напряжения s_i – положительны при растяжении;

касательные напряжения τ_i – положительны, если стремятся повернуть элемент по ходу часовой стрелки относительно точки, принадлежащей элементу.

Укажем на схеме (рис.3.7) положительные направления напряжений и рассмотрим равновесие выделенного элемента. Предварительно отметим, что на гранях элемента действуют напряжения, которые представляют собой интенсивность внутренних усилий. Уравнения же равновесия формируются для усилий, поэтому при их записи необходимо перейти от напряжений к усилиям, которые определяются как равнодействующие напряжений на гранях. Поскольку, из-за однородности НС элемента, распределение напряжений на гранях является равномерным, усилие, действующее по грани будет определяться как произведение соответствующего напряжения на площадь грани. В рассматриваемом случае площадь вертикальных граней равна dу ´1, горизонтальных – dх ´1. При записи уравнений единицу будем упускать.

Для плоской системы имеем три уравнения статики

, , .

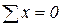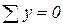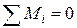Очевидно, что первые два уравнения тождественно удовлетворяются.

Уравнение моментов запишем относительно центра элемента (точки С)

.

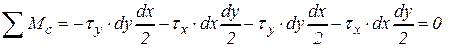Приводя подобные и сокращая на dх × dу, получим

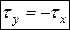. (3.1)

Формула (3.1) является аналитическим выражением закона парности касательных напряжений, который, при принятом правиле знаков, формулируется следующим образом: касательные напряжения, действующие по двум взаимно перпендикулярным площадкам, перпендикулярные к общему для них ребру, равны по величине и противоположны по знаку.

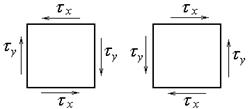
Из этого закона следует, что касательные напряжения на взаимно перпендикулярных площадках могут быть направлены либо к общему для площадок ребру, либо от ребра. Для элемента в этом случае возможны только две схемы направления касательных напряжений (см. рис.3.8).

Учитывая закон парности касательных напряжений плоское напряженное состояние можно характеризовать тремя напряжениями: s_x, s_y, и τ_y.

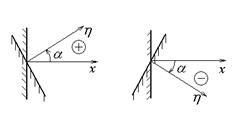
При исследовании напряжений на наклонных площадках наибольший интерес в случае плоского НС представляют напряжения в сечениях параллелепипеда, перпендикулярных координатной плоскости х0у. Положение этих площадок будем задавать углом между нормалью к площадке (h) и положительным направлением оси х (Ð a). Угол a считаем положительным, если поворот сечения осуществляется против движения часовой стрелки (рис.3.9).

Рис.3.8	Рис.3.9

Считая напряжения s_x, s_y, и τ_y заданными и положительными, определим напряжения (s_a, τ_a) на наклонной площадке, заданной произвольным углом a. Для этого рассечем элемент плоскостью, перпендикулярной к плоскости х0у, и повернутой относительно вертикальной грани на положительный угол a (рис.3.10). Правую часть элемента отбросим, заменив ее воздействие на левую часть (треугольный в плане элемент со сторонами: dS, dS ₁, dS ₂,) положительными нормальным (s_a) и касательным (τ_a) напряжениями, приложенными к наклонной площадке. Заметим, что исходные касательные напряжения на схеме заданы с учетом закона парности (см. рис.3.10).

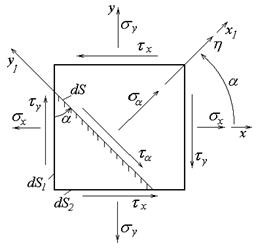
Рис.3.10

Рассмотрим равновесие треугольного элемента, введя дополнительные координатные оси х₁у₁ (вдоль нормали к наклонной площадке и в ее плоскости) (рис.3.10). Проектируя силы на эти оси, получим

,

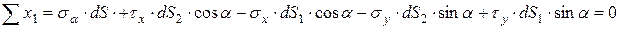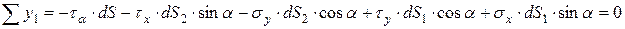
Выразим из первого уравнения s_a

.

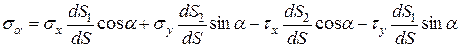Учитывая геометрические соотношения 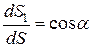и 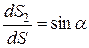, а также закон парности касательных напряжений (знак при замене t_х на t_у не меняем, поскольку он уже был учтен при расстановке исходных касательных напряжений на схеме элемента), будем иметь

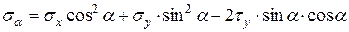
либо, с учетом тригонометрического соотношения ,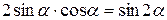

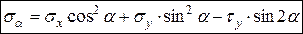. (3.2)

Выражая из второго уравнения равновесия t_a, используя те же подстановки, а также тригонометрическое соотношение

,

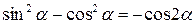окончательно получим

.

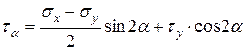Определим нормальное и касательное напряжения на площадке, которая перпендикулярна к заданной наклонной площадке (s_a+90° и t_a+90°, см. рис.3.11). Для этого подставим в полученные формулы для s_a и t_a значение угла a = a +90°. В результате такой подстановки получим

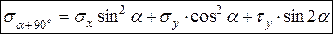, (3.3)

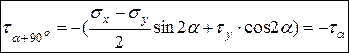. (3.4)

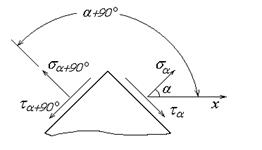
Рис.3.11

Таким образом, напряжения на двух взаимно перпендикулярных наклонных площадках, заданных произвольными углами a и a +90°, определяются следующими выражениями

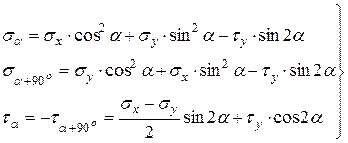. (3.5)

Складывая первые два выражения, получим

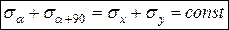. (3.6)

Соотношение (3.6) отражает важное свойство инвариантности суммы нормальных напряжений, действующих на взаимно перпендикулярных площадках: сумма нормальных напряжений, действующих на взаимно перпендикулярных площадках, не зависит от ориентации этих площадок в точке и является постоянной величиной. Отсюда следует, что экстремальные (максимальные и минимальные) нормальные напряжения будут действовать на взаимно перпендикулярных площадках.

Из соотношений (3.5) видно, что изменение угла a приводит к изменению величины нормальных и касательных напряжений. При определенных значениях угла напряжения достигнут экстремальных значений. С точки зрения оценки прочности конструкций, наибольший интерес представляют максимальные значения напряжений, положение площадок по которым они действуют, а так же значения главных напряжений и положение главных площадок. Очевидно, что математический анализ соотношений (3.5) позволяет все это определить, однако, прежде чем приступить к такому анализу, отметим одно интересное обстоятельство, связанное с рассматриваемыми соотношениями.

Сравним формулы (3.5) с выражениями для моментов инерции плоского сечения при повороте координатных осей (формулы (2.12) раздела «Геометрические характеристики плоских сечений»), которые приводим ниже (соотношения (3.5¢))

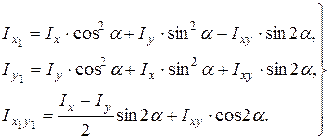(3.5¢)

Несмотря на различную физическую природу формул (3.5) и (3.5¢), математическая структура их абсолютно одинакова. Так, соотношения (3.5) можно получить из соотношений (3.5¢) формальной заменой

, , , , , .

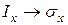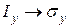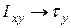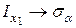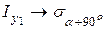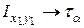Более того, независимая переменная в обоих случаях имеет одинаковый физический смысл (угол поворота a, который откладывается от положительного направления координатной оси х и положителен при повороте против хода часовой стрелки). Все это позволяет утверждать, что математический анализ соотношений (3.5) и (3.5¢) даст формально одинаковые результаты. Учтем это обстоятельство при проведении анализа формул (3.5).