Линейный SVM

Задачу можно сформулировать как поиск функции F(x), принимающей значения меньше нуля для векторов одного класса и больше нуля - для векторов другого класса. В качестве исходных данных для решения поставленной задачи, т.е. поиска классифицирующей функции F(x), дан тренировочный набор векторов пространства, для которых известна их принадлежность к одному из классов.

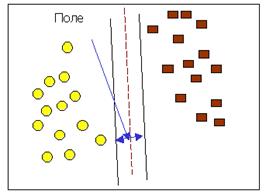
Рисунок 2.12 - Разделение классов прямой линией

Семейство классифицирующих функций можно описать через функцию F(x). Гиперплоскость определена вектором w и значением w₀, т.е. F(x)=(w,x)+w₀. Здесь (,) – скалярное произведение, w – нормальный вектор к разделяющей гиперплоскости, w₀ вспомогательный параметр. Те объекты, для которых F(x)>0 – один класс, F(x)<0 – другой класс.

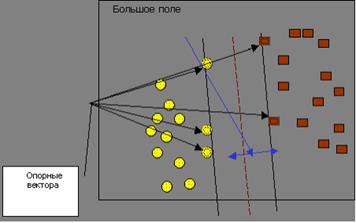
Рисунок 2.13 – Опорные векторы

Решение данной задачи проиллюстрировано на рис. 2.14. В результате решения задачи, т.е. построения SVM-модели, найдена функция, принимающая значения меньше нуля для векторов одного класса и больше нуля - для векторов другого класса. Для каждого нового объекта отрицательное или положительное значение определяет принадлежность объекта к одному из классов.

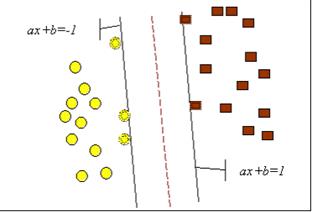
Рисунок 2.14 - Линейный SVM

Мы хотим выбрать такие w и w₀, которые максимизируют расстояние до каждого класса.

Можно посчитать, что данное расстояние равно 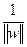. Проблема нахождения 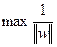эквивалентна проблеме нахождения 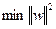. Имеем задачу оптимизации:

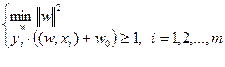
где 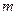- количество примеров в обучающей выборке.

Задача является задачей квадратичного программирования и решается методом множителей Лагранжа.

По теореме Куна-Такера эта задача эквивалентна двойственной задаче поиска седловой точки функции Лагранжа:

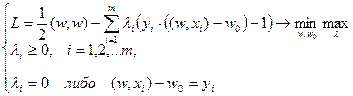
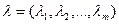- вектор двойственных переменных.

Необходимым условием седловой точки является равенство нулю производных Лагранжиана. Отсюда:

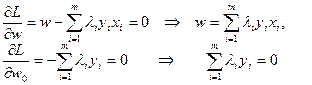
Искомый вектор является линейной комбинацией векторов обучающей выборки, причем, только тех, для которых 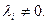На этих векторах 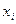ограничения-неравенства обращаются в равенства:

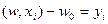, эти вектора называются опорными.

Подставляем два последних равенства в лагранжиан и получаем эквивалентную задачу квадратичного программирования, содержащую только двойственные переменные:

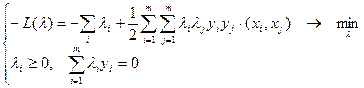
После решения последней задачи алгоритм классификации имеет вид: .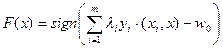

Следует помнить: сложность построения SVM-модели заключается в том, что чем выше размерность пространства, тем сложнее с ним работать. Один из вариантов работы с данными высокой размерности - это предварительное применение какого-либо метода понижения размерности данных для выявления наиболее существенных компонент, а затем использование метода опорных векторов.