Качественное исследование простейших моделей биологических процессов

Простейшим математическим моделям соответствует одно дифференциальное уравнение первого порядка:

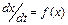(1)

Состояние системы, описываемое уравнением (1) в каждый момент времени характеризуется единственной величиной – значением переменной x в момент времени t.

Рассмотрим состояние равновесия, обозначив стационарную точку – .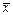

;

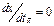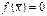
Если систему вывести из состояния равновесия, то она будет себя вести в соответствии с уравнением (1), описывающим ее поведение в области, где равновесия уже нет.

Устойчивое состояние равновесия можно охарактеризовать следующим образом: если при достаточно малом отклонении от положения равновесия система никогда не уйдет далеко от него, то состояние равновесия устойчиво и соответствует устойчивому режиму функционирования системы.

Если же система после выведения из состояния равновесия будет удаляться от него в соответствии с уравнением 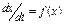, то это состояние является неустойчивым.

В случае одного уравнения вопрос об устойчивости состояния равновесия нетрудно решить, рассматривая график функции f(x).

По определению в стационарной точке правая часть уравнения ‑ функция f(x) обращается в нуль.

Здесь возможны три случая (рис. 2 а, б, в).

1. Вблизи состояния равновесия функция f(x) меняет знак с плюса на минус при возрастании x (рис. 2, а).

Отклоним изображающую точку системы в сторону 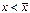. В этой области скорость изменения x dx/dt = f(x) положительна. Следовательно, x увеличивается, т.е. возвращается к 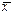. При 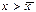скорость изменения величины x уменьшается, т.к. функция f(x)<0. Следовательно, здесь x уменьшается и опять стремится к 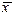. Таким образом, отклонения от стационарного состояния в обе стороны затухают. Стационарное состояние устойчиво.

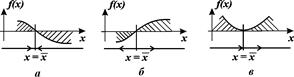
Рис. 2. Определение устойчивости стационарного состояния по графику функции f (x)

a – стационарное состояние 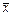устойчиво; б, в ‑ стационарное состояние 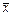неустойчиво

2. Вблизи состояния равновесия функция f (x) меняет знак с минуса на плюс при возрастании x (рис. 2, б).

Проведем рассуждения, аналогичные случаю 1. Поместим изображающую точку в область 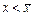, а затем в область 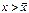. В обоих случаях изображающая точка удаляется от состояния равновесия. Стационарное состояние неустойчиво.

3. Вблизи состояния равновесия функции f(x) не меняет знак (рис 2, в).

Поскольку 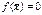, это означает, что изображающая точка, помещенная достаточно близко к состоянию равновесия с одной стороны, будет приближаться к нему, помещенная с другой стороны – удаляться. Стационарное состояние неустойчиво.