|
Определение. Неабелевая группа называется простой, если в ней всего две нормальные подгруппы - единичная и сама группа.
Приведем несколько примеров простых групп:
Теорема. Группы 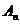 при при  простые. простые.
(группа  абелева, следовательно не простая; группа абелева, следовательно не простая; группа  содержит нормальную подгруппу содержит нормальную подгруппу  , следовательно не простая). , следовательно не простая).
Доказательство.
Лемма 1. Подгруппа  порождается тройными циклами. порождается тройными циклами.
Доказательство.
Мы знаем, что каждая подстановка есть произведение циклов длины 2 (транспозиций). Т.к. подстановки в  четны, то они равны произведению четного числа транспозиций. Рассмотрим произведение двух транспозиций: четны, то они равны произведению четного числа транспозиций. Рассмотрим произведение двух транспозиций:
 , если , если  различны, различны,
 , если , если 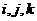 различны, различны,
 . .
Т.е. сгруппировав транспозиции по две, мы получим произведение циклов длины 3. 
Пусть в  существует нормальная подгруппа существует нормальная подгруппа 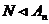 , причем , причем  . .
Лемма 2. Если 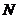 содержит тройной цикл ( содержит тройной цикл (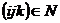 ), то ), то 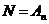 . .
Доказательство.
Возьмем произвольный тройной цикл  , возьмем , возьмем  , такую что , такую что  или или  , далее все элементы переходят в себя. Одна из таких подстановок будет четной, выберем ее. Получим , далее все элементы переходят в себя. Одна из таких подстановок будет четной, выберем ее. Получим  , т.к. , т.к.  . Следовательно подгруппе . Следовательно подгруппе 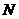 принадлежат все тройные циклы, следовательно (по лемме 1), принадлежат все тройные циклы, следовательно (по лемме 1),  . . 
Лемма 3. Если  содержит подстановку содержит подстановку  , у которой в разложении на независимые циклы встречается цикл длины , у которой в разложении на независимые циклы встречается цикл длины 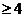 , то , то  . .
Доказательство.
Пусть  , тогда , тогда  . Т.е. . Т.е.  содержит цикл длины 3, следовательно (по лемме 2), содержит цикл длины 3, следовательно (по лемме 2), 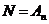 . . 
Лемма 4. Если 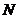 содержит подстановку содержит подстановку  , у которой в разложении на независимые циклы содержится хотя бы два цикла длины 3, то , у которой в разложении на независимые циклы содержится хотя бы два цикла длины 3, то  . .
Доказательство.
Пусть  , тогда , тогда  . Т.е. . Т.е.  содержит цикл длины 5, следовательно (по лемме 3), содержит цикл длины 5, следовательно (по лемме 3),  . . 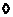
Лемма 5. Если  содержит подстановку содержит подстановку 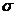 , у которой в разложении на независимые циклы содержится один цикл длины 3 и циклы длины 2, то , у которой в разложении на независимые циклы содержится один цикл длины 3 и циклы длины 2, то  . .
Доказательство.
Пусть  , тогда , тогда  , следовательно (по лемме 2), , следовательно (по лемме 2),  . . 
Лемма 6. Если 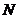 содержит подстановку содержит подстановку  , у которой в разложении на независимые циклы содержатся только циклы длины 2, то , у которой в разложении на независимые циклы содержатся только циклы длины 2, то  . .
Доказательство.
Если  , то, т.к. у нас не менее пяти символов, , то, т.к. у нас не менее пяти символов, 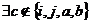 . Тогда . Тогда  , следовательно (по лемме 2), , следовательно (по лемме 2),  . .
Если  , то , то  , следовательно (по лемме 4), , следовательно (по лемме 4),  . .
Теперь, собственно, докажем теорему. Возьмем произвольную  . Она удовлетворяет условию одной из наших лемм, следовательно . Она удовлетворяет условию одной из наших лемм, следовательно  . Теорема доказана. . Теорема доказана. 
Приведем еще один пример простой группы: группа  - ортогональных симметричных матриц. - ортогональных симметричных матриц.
Определение. Коммутатором  элементов элементов  из группы из группы  называется элемент называется элемент 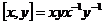 . .
Упражнение.  . .
Предложение. В  имеем имеем  , если , если  различны. различны.
Доказательство.
 . . 
Предложение. В группе  имеем имеем  , если , если  различны. различны.
Доказательство.


Определение. Коммутант группы -  (или (или  ) - это множество всех произведений коммутаторов. ) - это множество всех произведений коммутаторов.
Предложение.  . .
Доказательство.
Пусть  и и  , тогда , тогда
 . И, т.к. . И, т.к.  , то , то
 . Следовательно . Следовательно  - это подгруппа, докажем теперь ее нормальность. - это подгруппа, докажем теперь ее нормальность.
Пусть  , тогда , тогда  . .
 - снова коммутатор, следовательно - снова коммутатор, следовательно  равно произведению коммутаторов, т.е. равно произведению коммутаторов, т.е.  . . 
Теорема.
1)  при при  и и  при при  . .
2) 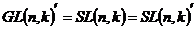 при при  . .
Доказательство.
1)  , ,  - четная подстановка, следовательно, - четная подстановка, следовательно,  . Более того мы доказали ранее, что . Более того мы доказали ранее, что  и что любая четная подстановка является произведением тройных циклов, т.е. произведением коммутаторов. Следовательно и что любая четная подстановка является произведением тройных циклов, т.е. произведением коммутаторов. Следовательно  . .
Имеем, что  , следовательно , следовательно 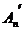 либо единичная, либо совпадает с либо единичная, либо совпадает с  . Но . Но  - это неабелевая группа, следовательно - это неабелевая группа, следовательно 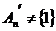 , следовательно , следовательно  . .
2) 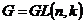 , ,  имеет определитель равный единице, следовательно имеет определитель равный единице, следовательно  . Более того мы знаем, что . Более того мы знаем, что  , если , если  . Следовательно . Следовательно  . Из этого же соображения получаем, что . Из этого же соображения получаем, что 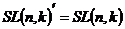 . . 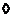
Упражнение. Докажите, что  . .
Лекция 6 (8.10.2001)
Предложение. Пусть  , тогда следующие условия эквивалентны: , тогда следующие условия эквивалентны:
1)  - абелева; - абелева;
2) 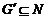 . .
Доказательство.
Напишем цепочку эквивалентных утверждений:  - абелева - абелева 
 . . 
|











