|
Теорема. Любая целочисленная прямоугольная матрица элементарными преобразованиями строк и столбцов приводится к диагональному виду 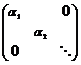 , где , где  . .
Доказательство. (по индукции по числу строк)
База индукции 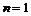 . Матрица имеет вид . Матрица имеет вид 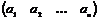 . Если она нулевая, то она уже имеет искомый вид. Если она не нулевая, то без ограничения общности можем считать, что . Если она нулевая, то она уже имеет искомый вид. Если она не нулевая, то без ограничения общности можем считать, что  - это наименьший по модулю ненулевой элемент (иначе переставим столбцы). Также мы можем считать, что - это наименьший по модулю ненулевой элемент (иначе переставим столбцы). Также мы можем считать, что  (иначе умножим столбец на (иначе умножим столбец на  ), таким же образом сделаем все элементы положительными. Пусть ), таким же образом сделаем все элементы положительными. Пусть 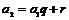 , где , где 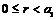 . Вычитая из второго столбца . Вычитая из второго столбца 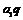 , получим строку , получим строку 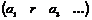 . Если . Если 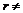 0, то наименьший модуль ненулевого элемента уменьшился, проделывая эту операцию несколько раз, получим, что модуль больше не может уменьшаться, т.к. он больше нуля. Следовательно, 0, то наименьший модуль ненулевого элемента уменьшился, проделывая эту операцию несколько раз, получим, что модуль больше не может уменьшаться, т.к. он больше нуля. Следовательно,  , и мы получим строку , и мы получим строку  . Проделав это несколько раз, мы в итоге получим строку . Проделав это несколько раз, мы в итоге получим строку  , поменяв местами столбцы, получим , поменяв местами столбцы, получим  - диагональная матрица, причем - диагональная матрица, причем  . .
Индуктивный переход. Пусть утверждение теоремы верно для 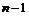 строк, докажем его для строк, докажем его для 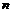 строк. Мы имеем матрицу строк. Мы имеем матрицу  Обозначим через Обозначим через  . Предположим, что привели . Предположим, что привели 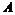 к к  так, что дальше так, что дальше 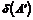 не уменьшается. Переставив строчки и столбцы и, если надо, умножив на не уменьшается. Переставив строчки и столбцы и, если надо, умножив на  , получим, что это минимум достигается на элементе , получим, что это минимум достигается на элементе 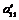 , причем , причем  . Тогда мы получим, что . Тогда мы получим, что  , если , если 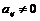 . .
Лемма. Все элементы первой строки  и первого столбца и первого столбца  делятся на делятся на  . .
Доказательство.
Возьмем произвольный элемент из первой строки  , получим, что , получим, что  , где , где 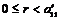 . Если . Если 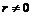 , то вычтя из , то вычтя из  -го столбца первый, умноженный на -го столбца первый, умноженный на 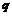 , получим на месте , получим на месте  число число 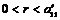 , следовательно , следовательно 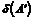 уменьшилось, что невозможно. Значит уменьшилось, что невозможно. Значит 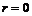 и все элементы первой строки делятся на и все элементы первой строки делятся на 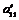 . Аналогично доказываем и про первый столбец. . Аналогично доказываем и про первый столбец. 
Раз все элементы первой строки и первого столбца делятся на 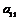 , то вычитая первую строку (умноженную на нужный коэффициент) из остальных, и вычитая первый столбец (умноженный на нужный коэффициент) из остальных, получим матрицу , то вычитая первую строку (умноженную на нужный коэффициент) из остальных, и вычитая первый столбец (умноженный на нужный коэффициент) из остальных, получим матрицу  , причем , причем 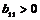 . Дальше, по предположению индукции, мы можем привести к диагональному виду матрицу . Дальше, по предположению индукции, мы можем привести к диагональному виду матрицу 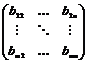 , состоящую из , состоящую из  строк. В итоге получим искомое разложение. строк. В итоге получим искомое разложение. 
Упражнение. Число  равно набольшему общему делителю всех элементов матрицы. равно набольшему общему делителю всех элементов матрицы.
Пример:
Приведем к диагональному виду матрицу  , имеем, что , имеем, что  НОДу всех элементов НОДу всех элементов 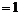 . Следовательно, . Следовательно,  можно получить (например, умножив первый столбец на можно получить (например, умножив первый столбец на  и прибавив к нему второй): и прибавив к нему второй):  , ну а дальше будем действовать по алгоритму из доказательства теоремы: , ну а дальше будем действовать по алгоритму из доказательства теоремы:
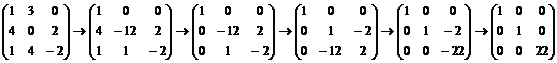 . .
Теорема. Пусть 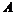 - свободная абелевая группа и - свободная абелевая группа и  - ее подгруппа, тогда в - ее подгруппа, тогда в  существует такой базис существует такой базис 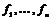 , что существуют , что существуют  , такие что , такие что 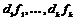 - базис в - базис в  . .
Доказательство.
Пусть 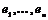 - базис в - базис в  . Пусть . Пусть  - базис в - базис в 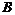 , тогда , тогда
 . Получим целочисленную матрицу . Получим целочисленную матрицу 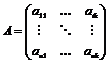 , приведем ее к диагональному виду , приведем ее к диагональному виду  . При проведении элементарных преобразований, мы просто перешли к новому базису в . При проведении элементарных преобразований, мы просто перешли к новому базису в 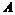 и в и в  , таким образом, мы нашли базис , таким образом, мы нашли базис  в в  , такой что , такой что  будет базисом в будет базисом в 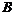 . . 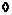
Вспомним определение конечно-порожденной абелевой группы и докажем
Теорема. Пусть  - конечно-порожденная абелевая группа, тогда - конечно-порожденная абелевая группа, тогда  является прямой суммой свободной абелевой группы и примарных циклических групп (циклических групп, порядок которых равен степени простого числа). является прямой суммой свободной абелевой группы и примарных циклических групп (циклических групп, порядок которых равен степени простого числа).
Доказательство.
Пусть  , т.е. , т.е.  порождена элементами порождена элементами 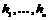 . . 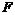 - свободная абелевая группа с базисом - свободная абелевая группа с базисом 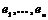 . Построим гомоморфизм . Построим гомоморфизм 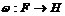 по правилу по правилу 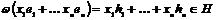 . Очевидно, что отображение . Очевидно, что отображение  сюръективно. Его ядро сюръективно. Его ядро  является подгруппой в является подгруппой в 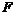 . Пусть . Пусть 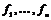 - базис в - базис в  , такой что , такой что 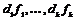 - базис в - базис в  (здесь (здесь  и и  ). В итоге имеем, что ). В итоге имеем, что

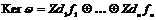 , здесь положим , здесь положим  при при  . .
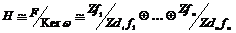 (по теореме о факторизации слагаемых). (по теореме о факторизации слагаемых).
Рассмотрим отдельное слагаемое  , следовательно , следовательно
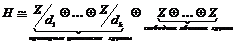 . Вообще говоря группы . Вообще говоря группы  могут быть и не примарными, но в этом случае они раскладывают дальше в прямую сумму примарных циклических групп. могут быть и не примарными, но в этом случае они раскладывают дальше в прямую сумму примарных циклических групп. 
Следствие. Конечная абелевая группа является прямой суммой примарных циклических групп.
Доказательство.
Любая конечная абелевая группа является конечно-порожденной. И т.к. свободная абелевая группа счетная, то ее нет в разложении, предложенном в теореме. Следовательно, остаются только примарные циклические группы. 
Пример.
Возьмем группу  порядка порядка  , тогда возможны следующие варианты: , тогда возможны следующие варианты:
1) 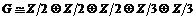
2) 
3) 
4) 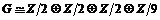
5) 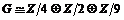
6) 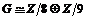
Следовательно всего существует 6 не изоморфных абелевых групп порядка  . .
Определение. Группа  не имеет кручения, если она не содержит неединичных элементов конечного порядка. не имеет кручения, если она не содержит неединичных элементов конечного порядка.
Теорема. Конечно-порожденная абелевая группа без кручения является свободной.
Доказательство.
По предыдущей теореме имеем, что  , следовательно этих слагаемых нет и , следовательно этих слагаемых нет и  - свободная абелевая группа. - свободная абелевая группа. 
|

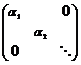 , где
, где  Обозначим через
Обозначим через  так, что дальше
так, что дальше  , причем
, причем 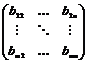 , состоящую из
, состоящую из  , имеем, что
, имеем, что  , ну а дальше будем действовать по алгоритму из доказательства теоремы:
, ну а дальше будем действовать по алгоритму из доказательства теоремы: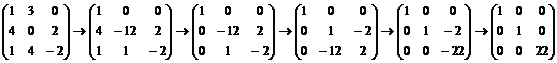 .
. . Получим целочисленную матрицу
. Получим целочисленную матрицу 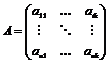 , приведем ее к диагональному виду
, приведем ее к диагональному виду  . При проведении элементарных преобразований, мы просто перешли к новому базису в
. При проведении элементарных преобразований, мы просто перешли к новому базису в  , следовательно
, следовательно 








