|
Определение. Пусть 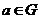 . Циклической подгруппой . Циклической подгруппой  , порожденной элементом , порожденной элементом 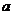 , называется множество , называется множество  . . Это определение корректно, т.к.  - снова степень - снова степень 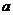 , , 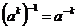 - снова степень - снова степень 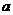 . . Определение. Группа  - циклическая, если - циклическая, если  такой, что такой, что  . . Примеры циклических групп:
1) 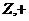 , т.к. , т.к.  ; ;
2)  , где , где 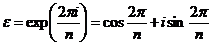 . . Теорема. Пусть 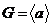 , тогда , тогда  . .
Доказательство.
Допустим, что найдутся такие  , что , что  . Тогда . Тогда  и и  . Следовательно, порядок элемента . Следовательно, порядок элемента  конечен конечен 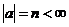 . Пусть . Пусть  и и  , тогда , тогда  . Следовательно, группа . Следовательно, группа  состоит из элементов состоит из элементов 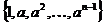 . Докажем, что они все различны. Пусть . Докажем, что они все различны. Пусть 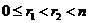 и и 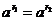 , тогда , тогда  и и 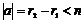 . Получили противоречие, следовательно . Получили противоречие, следовательно  , все элементы различны и всего из , все элементы различны и всего из 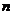 штук, т.е. штук, т.е. 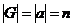 . .
Если же все степени  будут различны, то будут различны, то  . . 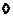 Теорема. Любая подгруппа циклической группы сама является циклической.
Доказательство.
Пусть  . Тогда . Тогда 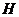 состоит из каких-то степеней элемента состоит из каких-то степеней элемента 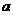 . Заметим, что если . Заметим, что если  , то и , то и  . Если . Если  , то , то  . Если же . Если же  содержит не только единичный элемент, то содержит не только единичный элемент, то 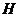 содержит какой-то элемент содержит какой-то элемент  , где , где 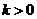 (в силу нашего замечания выше). Пусть (в силу нашего замечания выше). Пусть 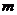 - наименьшее натуральное число такое, что - наименьшее натуральное число такое, что 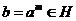 . Пусть . Пусть 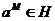 и и  , где , где 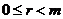 . Тогда . Тогда 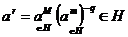 . Если . Если  , то мы получаем противоречие с выбором числа , то мы получаем противоречие с выбором числа  , следовательно, , следовательно, 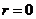 и и  . Следовательно . Следовательно  . . 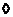 Следствие 1. Пусть 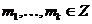 и и  , тогда , тогда 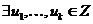 такие, что такие, что  . . Следствие 2. Пусть  (порядка (порядка  ) и ) и 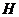 - подгруппа в - подгруппа в  , тогда , тогда  , причем , причем 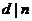 . .
Доказательство.
По теореме 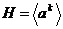 . Пусть . Пусть 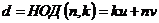 , тогда , тогда  . Следовательно . Следовательно 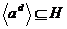 . Докажем теперь включение в другую сторону. Пусть . Докажем теперь включение в другую сторону. Пусть  , но , но  , следовательно , следовательно  . Следовательно . Следовательно 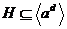 , т.е. , т.е.  , причем , причем  . .  Упражнение. Докажите, что  , где , где 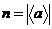 . .
|










