|
При охлаждении тело отдает во внешнюю среду теплоту. q – количество теплоты, отданное телом за время 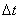 , определяется формулой: , определяется формулой:
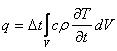 , (1) , (1)
где c – удельная теплоемкость,
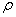 - плотность, - плотность,
Т – температура образца.
С другой стороны, если считать, что теплота отдается во внешнюю среду только через S – поверхность образца, то q выражается формулой:
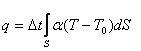 , (2) , (2)
где 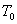 - температура окружающей среды; - температура окружающей среды;
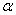 - коэффициент теплоотдачи, зависящий от свойств поверхности и окружающей среды. - коэффициент теплоотдачи, зависящий от свойств поверхности и окружающей среды.
Из (1) и (2) получим:
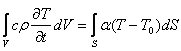 . (3) . (3)
Если считать, что 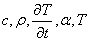 не зависят от координат, то после интегрирования выражения (3) имеем: не зависят от координат, то после интегрирования выражения (3) имеем:
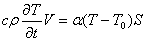 . (4) . (4)
Выражение (4) может быть преобразовано к виду:
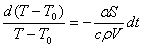 . (5) . (5)
Интегрируем:
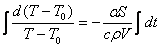
Отсюда:
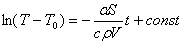 (6) (6)
Интегрирование возможно лишь в том случае, когда выражение 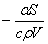 не зависит от температуры. Это выполняется приближенно при малых изменениях разности не зависит от температуры. Это выполняется приближенно при малых изменениях разности 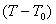 . .
Уравнение (6) в координатах 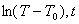 представляет собой прямую линию с угловым коэффициентом представляет собой прямую линию с угловым коэффициентом 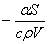 . .
Построим такие прямые для двух образцов одинаковых форм и размера, но изготовленных из разных металлов. Для одного образца угловой коэффициент равен:
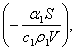 для другого - для другого - 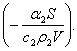
Отношение угловых коэффициентов:
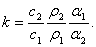
Поверхность образцов можно обработать так, чтобы 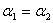
Тогда:
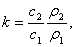 (7) (7)
и если теплоемкость одного из образцов известна (например, 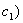 , то теплоемкость другого определяем по формуле: , то теплоемкость другого определяем по формуле:
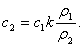 (8) (8)
Выполнение работы
Схема установки изображена на рис.
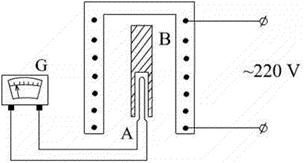
рис.
Электропечь может перемещаться по двум направляющим стержням в вертикальном направлении. Образец B представляет собой цилиндр с высверленным с одного конца каналом. Этим каналом образец помещают на фарфоровую трубку с термопарой А. Концы термопары подведены к гальванометру G. Температура образца отсчитывается по шкале гальванометра, для чего последний снабжен графиком перевода его показаний в значение температуры спая термопары.
В начале опыта печь опускается по направляющим стержням вниз настолько, чтобы образец полностью оказался внутри нее, после чего включается источник тока. После нагрева образца до некоторой заданной температуры печь быстро поднимается вверх. Нагретый образец охлаждается в неподвижном воздухе.
Через каждые 10-15 сек записывается температура образца по показаниям гальванометра. После охлаждения образца до температуры ниже 100 0С опыт повторяют.
Для каждого образца снимают две кривые охлаждения, чтобы убедиться, что нет случайного искажения кривых.
Эталоном служит образец из меди с известной зависимостью теплоемкости от температуры.
По ряду полученных из опыта значений температуры для каждого образца составляют таблицу:
N |
t сек |
деления гальванометра |
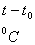
|
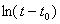
|
|
|
|
|
|
Строят графики зависимости 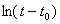 от t для исследуемых образцов Полученные графики разбивают на такие участки, где зависимость от t для исследуемых образцов Полученные графики разбивают на такие участки, где зависимость 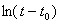 от t можно считать линейной. Для каждого из таких участков определяют тангенс угла наклона прямой к оси времени и вычисляют значение теплоемкости исследуемого образца по формуле (8). Значения теплоемкости меди при разных температурах берут из приложенного графика. от t можно считать линейной. Для каждого из таких участков определяют тангенс угла наклона прямой к оси времени и вычисляют значение теплоемкости исследуемого образца по формуле (8). Значения теплоемкости меди при разных температурах берут из приложенного графика.
По полученным данным строят график зависимости теплоемкости материала образца от температуры.
|

