· Если F есть первообразная для f, а G – первообразная для g, то F + G есть первообразная для f + g.
· Если F есть первообразная для f, а k – постоянная, то kF есть первообразная для kf.
· Если F(x) есть первообразная для функции f(x), а k и b – постоянные, причём 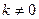 , то
, то 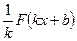 есть первообразная для функции f(kx + b).
есть первообразная для функции f(kx + b).
Ф о р м у л ы:
Если f(x) = k, то F(x) = kx + C; Если f(x) = 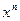 , то F(x) =
, то F(x) = 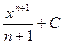 ;
;
Если f(x) = sin x, то F(x) = -cos x + C; Если f(x) = cos x, то F(x) = sin x + C;
Если f(x) = 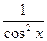 , то F(x) = tg x + C; Если f(x) =
, то F(x) = tg x + C; Если f(x) = 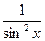 , то F(x) = - ctg x + C;
, то F(x) = - ctg x + C;
Если f(x) = 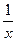 , то F(x) = ln
, то F(x) = ln 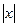 + C; Если f(x) =
+ C; Если f(x) = 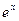 , то F(x) =
, то F(x) = 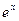 + C;
+ C;
Если f(x) =a 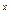 , то F(x) =
, то F(x) = 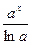 + C;
+ C;
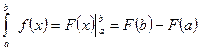 - формула Ньютона – Лейбница.
- формула Ньютона – Лейбница.
y = 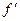 (x
(x 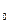 )(x
)(x 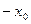 ) +
) + 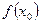 - уравнение касательной
- уравнение касательной
Г Е О М Е Т Р И Я.
Планиметрия.
· Сумма смежных углов равна 180 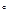 .
.
· Вертикальные углы равны.
· Сумма углов треугольника равна 180 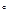 .
.
· Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
· В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов, т.е. 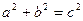
· 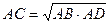 , где АВ – гипотенуза, АС – катет, AD – проекция катета АС на гипотенузу.
, где АВ – гипотенуза, АС – катет, AD – проекция катета АС на гипотенузу.
· CD = 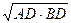 , где AD,BD – проекции катетов на гипотенузу, CD – высота проведённая к гипотенузе.
, где AD,BD – проекции катетов на гипотенузу, CD – высота проведённая к гипотенузе.
· Теорема косинусов: 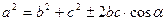 , где a,b,c – стороны треугольника,
, где a,b,c – стороны треугольника, 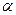 - угол между b и c, ставим «+», если
- угол между b и c, ставим «+», если 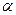 - тупой угол и «-», если
- тупой угол и «-», если 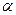 - острый угол.
- острый угол.
· Теорема синусов: 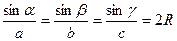
· 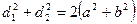 , где a,b – стороны параллелограмма,
, где a,b – стороны параллелограмма, 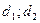 - его диагонали.
- его диагонали.
· 180 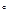 (n-2) – сумма углов многоугольника.
(n-2) – сумма углов многоугольника.
· 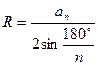 ;
; 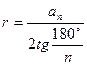 , где R – радиус описанной окружности, r – радиус вписанной окружности,
, где R – радиус описанной окружности, r – радиус вписанной окружности, 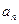 - сторона правильного многоугольника.
- сторона правильного многоугольника.
· 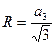 ;
; 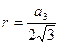 ;
; 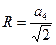 ;
; 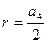 ;
; 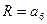 ;
; 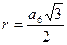 .
.
 2015-05-25
2015-05-25 375
375








