Функции отсчетов для заданного сигнала будут

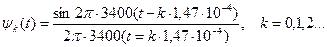
Тогда ряд Котельникова можно записать в виде

u(t)=1,0y₀(t)+2,6y₁(t)+3,5y₂(t)+…-1,5y₈(t)-1,3y₉(t).

Проверить, что сумма девяти членов ряда дает непрерывный сигнал u(t), мож­но суммированием ряда, как проделано это на рис. 2.12,б. То, что в отсчетных точках ряд и непрерывный сигнал совпадают, очевидно. Теорема Котельникова доказывает, что такое же совпадение имеется на всей оси t.

Физический смысл теоремы Котельникова. Теорема Котельникова утверждает, что если требуется передать непрерывный сигнал u(t) с ограниченным спектром по каналу свя­зи, то можно не передавать все его значения: достаточно передать мгновенные значения (отсчеты) через интервал Dt.. Поскольку сигнал u(t) полностью определяется этими значениями, по ним он может быть восстановлен на приемном конце системы связи. Для этого достаточно соединить отсчеты плавной кривой, как это сде­лано на рис. 2.12. Это объясняется тем, что сигнал u(t) между от­счетами может изменяться только плавно, так как частоты выше F_m, дающие быстрые (скачкообразные или колебательные) изме­нения, в сигнале отсутствуют. Ведь отсчеты берутся достаточно часто, и тем чаще, чем выше максимальная частота F_m.

Практическое применение теоремы Котельни­кова. Для применения теоремы Котельникова в технике связи необходимо указать технические способы дискретизации сигнала и восстановления его по отсчетам. Дискретизация осуществляется просто: периодически на короткое время через интервал Dt клю­чом замыкаем цепь от источника сигнала u(t) к нагрузке — по­лучаем отсчеты u(kDt). Ряд Котельникова (2.14) указывает спо­соб восстановления сигнала u(t) по отсчетам: каждый отсчет ум­ножить на функцию отсчетов y_k(t) и произведение просуммиро­вать. Поскольку функция отсчетов y_k(t) является импульсной ре­акцией идеального фильтра нижних частот (ФНЧ), то, подавая отсчеты u(kDt) на вход идеального ФНЧ с верхней частотой про­пускания F_m, на выходе фильтра получим исходный непрерывный сигнал u(t). Фильтр выполнит как операцию формирования функ­ции отсчетов y_k(t) и операции умножения и суммирования во времени.

Структурная схема передачи непрерывного сигнала u(t) на ос­нове теоремы Котельникова показана на рис. 2.13. На передающей стороне берутся отсчеты u(kDt) сигнала u(t) в моменты kDt

Рис. 2.13. Структурная схема системы связи с использованием ряда Котельни­кова

Далее отсчеты любым способом передаются по каналу связи. Иде­альный ФНЧ на приемном конце восстанавливает исходный сиг­нал u(t). Приведенная схема реализует так называемый импульс­ный способ передачи непрерывных сигналов.

Таким образом, в основе любых импульсных способов переда­чи лежит теорема Котельникова. Именно она указывает, при ка­ких условиях передача непрерывного сигнала может быть сведена к передаче последовательности импульсов. Частота следования импульсов, называемая также частотой дискретизации, определя­ется по теореме Котельникова:

F_д=1/Dt=2F_m. (2.15.)

Однако при практическом применении теоремы Котельникова имеются ограничения. Во-первых, теорема требует, чтобы спектр сигнала не превышал частоту F_m, во-вторых, для восстановления сигнала по отсчетам предполагается применение идеального ФНЧ. На практике же не существует ни сигналов с ограниченным спект­ром, ни идеальных фильтров. Любой реальный сигнал имеет ко­нечную длительность и соответственно бесконечный спектр. Иде­альные фильтры со строго ограниченной полосой пропускания физически нереализуемы. Поэтому, строго говоря, восстановление непрерывного сигнала по последовательности отсчетов осуществи­мо только с некоторой погрешностью, которая возникает из-за то­го, что неограниченные спектры непрерывного сигнала F(f) (рис. 2.14,а) и отсчетов F_m(f) перекрываются и никаким фильтром их не разделить. Это показано на рис. 2.14,6. Спектр сигнала F(f) в принципе неограниченный, а частота дискретизации f_д1 выбира­лась по какой-то условной максимальной частоте F_m. Для умень­шения перекрытия спектров и соответственно погрешности восста­новления сигнала реальным ФНЧ с передаточной функцией H(f)

Рис.2.14. Спектры сигнала u(t) и его отсчетов: a —спектр сигнала; б — спектр отсчетов при f_{д <}2F_m; в — спектр отсчетов

при f_д > 2F_m следует частоту дискретизации выбирать на 10... 15% выше теоре­тической (2.15), рассчитываемой по теореме Котельникова (рис. 2.14,в). Так, например, поступили при выборе частоты дискрети­зации для речевого сигнала при F_m=3400 Гц в системах с им­пульсной передачей. По теореме Котельникова согласно (2.15) f_д = 2*3400 = 6800 Гц. Рекомендовано же МККТТ f_д._р = 8000 Гц и, соответственно,Dt_p=1/f_д.р.=125*10^-6с=125мкс.

Теорема котельникова в многоканальной электросвязи. Возможность передачи вместо непрерывных сигналов последовательных импульсов (отсчетов), доказанная в теореме Котельникова, позволяет осуществить временное разделе­ние. Дело в том, что при импульсной передаче период следования импульсов обычно намного больше их длительности или, как гово­рят, импульсы имеют большую скважность — при большой скваж­ности между импульсами одного сигнала остается промежуток, на котором можно разместить импульсы от других сигналов. Это и есть временное разделение. В настоящее время уже реализованы многоканальные системы с временным разделением 12, 15, 30, 120, 480 речевых сигналов.

Принцип временного разделения двух сигналов U₁(t) и U₁(t) поясняет рис. 2.15. Отсчеты как первого (рис. 2.15,б), так и вто­рого (рис. 2.15,в) сигналов берутся через одинаковый интервал Dt, но с таким сдвигом t во времени, что они не перекрываются.

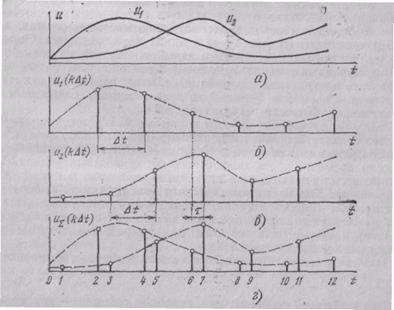
Рис. 2.15. К пояснению принципа временного разделения:

а — непрерывные сигналы; б —отсчеты первого сигнала; в — отсчеты второго сигнала-г —суммарная последовательность отсчетов двух сигналов, передаваемая по каналу связи

Результирующая суммарная последовательность импульсов u_S(kDt), передаваемая по линии связи, несет информацию как о первом, так и о втором сигнале (рис. 2.15,г). Для разделения сиг­налов на приемном конце достаточно произвести коммутацию: четные импульсы направить к одному ФНЧ, нечетные — к дру­гому.