Теорема и ряд В. А. Котельникова

Разложение непрерывных сигналов вряд Ко­тельников а. Все реальные непрерывные сигналы являются плавными функциями времени. Скачки значений в них практиче­ски не наблюдаются. Поэтому такие сигналы можно представить последовательностью их значений, взятых с некоторым шагом по времени. Значение сигнала в фиксированный момент называется отсчетом.

На рис. 2.10 представлен непрерывный сигнал и его отсчеты с различным шагом по времени. При малом шаге (рис. 2.10,а) по­следовательность отсчетов достаточно точно описывает сигнал, при большом шаге (рис. 2.10,6) по отсчетам нельзя восстановить форму сигнала, так как пропущены его характерные экстремальные точки.

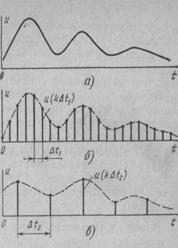Рис. 2.10. Представление сигнала отсче­тами (дискретизация сигнала): а —

непрерывный сигнал; б—малый шаг дис­кретизации; в — большей шаг дискретизации

Возникает вопрос: как часто следует брать отсчеты, чтобы по ним можно было полностью восстановить сигнал?

Ответ дает теорема, доказан­ная в 1933 г. советским ученым академиком В. А. Котельниковым и названная его именем. Со­гласно этой теореме любой сиг­нал u(t), не содержащий частот выше F_m, можно точно восстано­вить по его отсчетам u(kDt), взя­ тым через интервалы Dt= 1/2F_m. Восстановление сигнала осуществ­ляется с помощью ряда

u(t)= 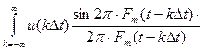(2.14)

Доказательство теоремы дано в Приложении 4.

Ряд, определяемый выражением (2.14), называется рядом Ко-тельникова. В нем коэффициенты разложения u(kDt) равные

мгновенным значениям непрерывного сигнала u(t) в моменты являются отсчетами сигнала u(t), а функции

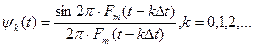
— функциями отсчетов, которые имеют одинаковую форму функ­ции типа sinx/x и отличаются друг от друга временным сдвигом на интервал kDt. Графики функций y_k(t) и их особые точки (максимумы, минимумы, пересечения с осями координат) показаны на рис. 2.11. Функции отсчетов y_k(t) представляют собой импульсную реакцию идеального ФНЧ с граничной частотой

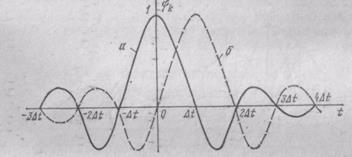
Рис 2.11. Функции отсчетов:

a-y₀(t); б--y₀(t-Dt)

F_m, если на его вход подавать б-функцию в момент kDt.

Теорема Котельникова является основой для дискретизации непрерывных сигналов по времени, так как, во-первых, доказы­вает, что непрерывный сигнал можно заменить его дискретными значениями, во-вторых, дает правило вычисления шага дискрети­зации — Dt=1/2F_m. При таком шаге дискретизации ряд Котель­никова дает точное временное представление сложного сигнала. Иногда возникает вопрос, каким рядом (Фурье или Котельнико­ва) лучше пользоваться для математического описания сложного сигнала? Однозначного ответа дать нельзя — все зависит от кон­кретно решаемой задачи. Единственное, что можно отметить, — простоту вычислений коэффициентов разложения a_k в ряде Ко­тельникова.

Пример 2.5. Представить в виде ряда Котельникова отрезок речевого сигна­ла, осциллограмма которого показана на рис. 2.12,а. Спектр этого сигнала со­средоточен в полосе 300... 3400 Гц.

По максимальной частоте спектра сигнала f_m=3400 Гц определяем шаг дискретизации Dt= l/2F_m= 1/2-3400 =1,47-10^-4 с. На оси времени откладываем моменты t, начиная с произвольного, например с=0, через интервал DtДа­лее определяем отсчеты сигнала в эти моменты. Из временной диаграммы сиг­нала (осциллограммы), изображенной на рис. 2.12,а, следует:

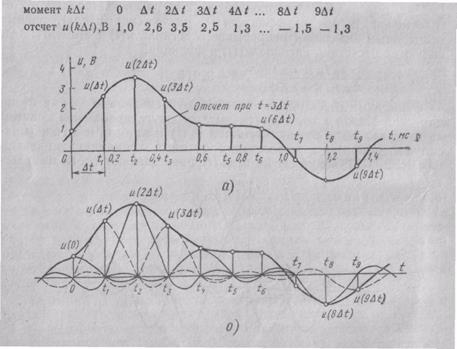
Рис. 2.12. Представление сигнала рядами Котельникова:

а —сигнал u(t) и его отсчеты; б —сумма ряда Котельникова