Случайные сигналы, помехи

Основные понятия. Главное отличие случайных сигна­лов от детерминированных состоит в том, что после наблюдения их на конечном отрезке времени t_н нельзя предсказать их буду­щее. Все случайные сигналы и помехи являются непредсказуемы­ми. Таким образом, для случайных сигналов нельзя подобрать математическую формулу, по которой можно было бы рассчитать их мгновенные значения.

Случайные сигналы и помехи относятся к тем случайным яв­лениям природы, изменением основных закономерностей которых занимается теория вероятностей. Одна из задач, решаемых тео­рией вероятностей, — нахождение таких характеристик случайных явлений, которые были бы неслучайными и позволяли проводить математические расчеты случайных явлений. Исследование осуще­ствляется статистическими методами, для которых характерен принципиальный отказ от определения результатов каждого от­дельного опыта и переход к рассмотрению массовых опытов, т. е. опытов, совершаемых много раз в одних и тех условиях. Опреде­ляемые при этом характеристики называются статистическими.

Все случайные явления, изучаемые в теории вероятностей, мож­но разбить на три типа: случайные события, случайные величины и случайные процессы. Каждый из этих типов случайных явлений имеет свои особенности и характеристики.

Реальные случайные сигналы и помехи, как и детерминирован­ные, могут быть простыми и сложными, аналоговыми, дискретны­ми и цифровыми. Вообще-то все они дискретные или непрерывные функции времени, но, в зависимости от конкретных условий, их можно рассматривать и как случайные величины, и как случай­ные события. Для их математического описания, т. е. выбора ма­тематической модели сигнала, необходимо решить две задачи: 1) к какому типу случайных явлений отнести случайный сигнал (помеху) в конкретной ситуации и 2) определить необходимые статистические характеристики.

Напомним важнейшие понятия теории вероятностей, необходи­мые для выбора математической модели случайных сигналов и по­мех.

Случайные события. Случайное событие — это всякий факт, который в результате опыта может произойти или не прои­зойти. Это и передача текста без ошибок, и работа канала связи без повреждений не менее Т часов, и превышение помехой заданного уровня и т. д. Обозначаются случайные события начальными прописными буквами латинского алфавита: А, В, С.

Числовыми характеристиками степени возможности появления события в тех или иных условиях опыта являются частота появ­ления события и вероятность события.

Частота появления события в данной серии опытов — это от­ношение числа m опытов, в которых появилось событие А, к об­щему числу опытов n:

n=m/n.

Вероятность события

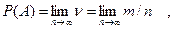(2.16)

т. е. вероятность случайного события Р(А) есть частота его появ­ления при неограниченном увеличении числа независимых одно­родных опытов n. Это доказал швейцарский математик Я. Бернул-ли. С достаточной для практических вычислений точностью можно считать, что если число опытов m, в котором появилось событие А, больше 20, то частота случайного события n численно совпадает с его вероятностью Р(А). Так, если из 50 принятых знаков два ошибочных, то частота ошибок n=2/50=4*10^-2, если зафиксиро-

вано 40 ошибочных знаков из 1 тыс. принятых, то можно считать, что вероятность ошибки знака Р(А) =40/1000 = 4*10^-2.

Случайные величины. Величина, значение которой ме­няется от опыта к опыту случайным образом, называется случай­ной. В отличие от неслучайных (детерминированных) величин, для случайной величины нельзя предсказать точно, какое она при­мет значение в условиях опыта. Число ошибок в тексте, число занятых каналов многоканальной системы связи, уровень помехи в канале, мощность сигнала на выходе линии связи — это все примеры случайных величин. Можно даже сказать так: реальнос­ти мира таковы, что любая физическая величина является слу­чайной.

Обозначаются случайные величины прописными буквами латин­ского алфавита X, Y, Z, а значения, которые они принимают, —• строчными буквами х, у, z.

Случайные величины делятся на дискретные и непрерывные. Дискретная случайная величина X может принимать только конеч­ное множество значений х₁, х₂,..., х_n, непрерывная — любые зна­чения х из некоторого интервала, даже бесконечного.

Для математического описания случайных величин вводятся следующие неслучайные основные статистические характеристики:

1. Функция распределения вероятности

F(x)=P(X£x), (2.17)

показывающая вероятность того, что значения случайной величи­ны X не превысят конкретно выбранного значения х. Если слу­чайная величина X принимает дискретные значения, то F(x)- дискретная функция. Если X — непрерывная случайная величина, то F(х) — монотонно возрастающая функция, значения которой лежат в интервале 0£F(x)£l, причем F(-¥)=0, F(¥)=1.

2. Плотность распределения вероятности р (х) (или, короче,
плотность вероятности), которая вычисляется как производная от
функции распределения

p(x)=dF(x)ndx.

Физически р(х) есть вероятность попадания случайной величины в малый интервал dx в окрестности точки х. Взаимосвязь между р(х) и F(x) определяется выражением

F(x)= 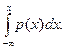(2.18)

3. Математическое ожидание

M(X)= 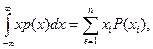(2.19)

которое по своему смыслу является средним значением случай­ной величины. Так, если X — случайное напряжение (ток), то М(Х) — среднее значение, или постоянная составляющая напря­жения (тока). В (2.19) интегрирование применяется при вычис­лениях М(Х) — непрерывной случайной величины, причем р(х) — плотность вероятности: суммирование — при вычислениях М(Х) — дискретной случайной величины и х_i — значения случайной вели­чины, Р(хi) — вероятности этих значений.

4. Дисперсия D(X), или s²x количественно характеризующая
степень разброса результатов отдельных опытов относительно
среднего значения. Вычисляется как математическое ожидание
квадрата отклонения случайной величины от своего математичес­
кого ожидания

D(X)=s²x=M[X-V(X)]²=M(X²)-M²(X). (2.20)

Величина s_x т. е. квадратный корень из дисперсии, называется среднеквадратическим отклонением. По физическому смыслу это есть то, что в электротехнике называется эффективным значе­нием.

Случайные процессы. Случайный процесс X(t) — это такая функция времени t, значения которой при любом фиксиро­ванном значении аргумента t являются случайней величиной. Из этого определения следует, что если будет производиться наблю­дение изменения во времени любой случайной величины X, то это уже будет случайный процесс X(t). Напряжение шума на выходе линии связи, температура воздуха, ток на выходе микрофона при разговоре и т.д., если производится наблюдение за мгновенными значениями перечисленных физических величин во времени, явля­ются примерами случайных процессов.

Отдельные наблюдения над случайным процеcсом, протекаю­щим в одинаковых условиях опыта, дают каждый раз различные

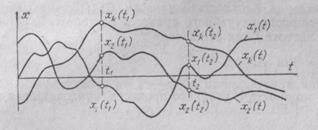
Рис. 2.16. Реализация случайного процесса X(t)

функции X_h(t) — различные экземпляры или реализации случай­ного процесса. Совокупность {x_k(t)} всех возможных реализаций данного случайного процесса называется ансамблем. Таким ан­самблем может служить набор сигналов Х₁(t), x₂(t),..., Xk(t), наблюдаемых одновременно на выходах многоканальной системы связи (рис. 2.16). Совсем не обязательно, чтобы реализации слу­чайного процесса были сложными функциями, как показано на рис. 2.16. Гармонический сигнал U_mcos(wt+y), у которого хотя бы один из параметров U_m,w,y - случайная величина, также является случайным процессом.

Случайные процессы бывают различных типов. Однако в электросвязи большинство случайных сигналов и помех относятся к стационарным эргодичес-ким случайным процессам. Случайный процесс является стационарным, если та­кие его характеристики, как функция распределения F(x), плотность вероятно­сти р(х), математическое ожидание М(Х), дисперсия D(X) не зависят от вре­мени. Определяются они точно так же, как и для случайной величины.

Эргодическими стационарными называются такие случайные процессы, у которых усреднение по времени одной реализации приводит к тем же резуль­татам, что и статистическое усреднение по всем реализациям. Физически это означает, что все реализации эргодического процесса похожи друг на друга, поэтому измерения и расчеты характеристик такого процесса можно проводить по одной (любой) из реализаций, что значительно проще.

Кроме четырех вышеперечисленных характеристик — функции распределения F(x), плотности вероятности р(х), математическо­го ожидания М(Х), дисперсии D(X) — для описания случайного процесса применяются еще две: функция корреляции K_x(t) и

спектральная плотность мощности G_x(f) или G_x(w).

Функция корреляции K_x(t)характеризует степень взаимосвязи

между значениями случайного процесса в различные моменты t и t+t.Для эргодического процесса K_x(t)вычисляется усредне-

нием по времени произведения

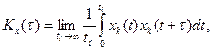(2.21)

где t_н — время наблюдения реализации Xk(t)

Спектральная плотность мощности Gx(f) показывает распре­деление мощности случайного процесса по частотам. Определяется на любой частоте f как отношение

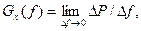(2.22)

где DP— мощность случайного процесса, приходящаяся на полосу частот Df.