 1. Рассчитайте ширину запрещенной зоны полупроводника, который содержит
1. Рассчитайте ширину запрещенной зоны полупроводника, который содержит 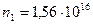 см-3 электронов за Т1=400 К и n2=5,5·1015 см-3 за Т2=300 К. Ширина запрещенной зоны изменяется с температурой по линейному закону.
см-3 электронов за Т1=400 К и n2=5,5·1015 см-3 за Т2=300 К. Ширина запрещенной зоны изменяется с температурой по линейному закону.
Дано: Решение:
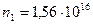 см-3
см-3 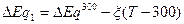
Т1=400 К 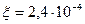 (эВ/К) – табличные данные
(эВ/К) – табличные данные
n2=5,5·1015 см-3 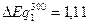 (эВ) – табличные данные
(эВ) – табличные данные
 Т2=300 К
Т2=300 К 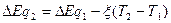
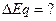
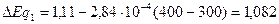 (эВ)
(эВ)
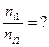
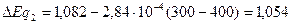 (эВ)
(эВ)
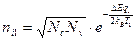 ,
, 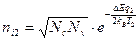
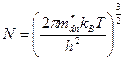
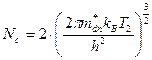 ,
, 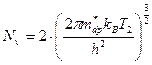
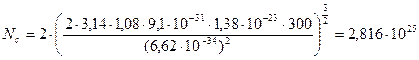 (м-3)
(м-3)
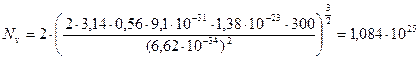 (м-3)
(м-3)
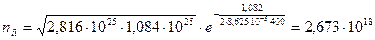 (м-3)
(м-3)
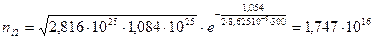 (м-3)
(м-3)
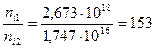
 2. В кристаллах арсенида галлия растворено 10-5 ат% телуру. Найдите положение уровня Ферме относительно середины запрещенной зоны за Т=500 К. При расчетах использовать такие данные: плотность GaAs
2. В кристаллах арсенида галлия растворено 10-5 ат% телуру. Найдите положение уровня Ферме относительно середины запрещенной зоны за Т=500 К. При расчетах использовать такие данные: плотность GaAs 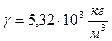 ; ширина запрещенной зоны
; ширина запрещенной зоны 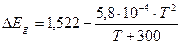 ; эффективные массы плотности состояний
; эффективные массы плотности состояний 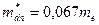 ,
, 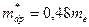 .
.
Дано: Решение:
Т=500 К 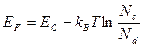 (эВ)
(эВ)
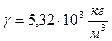
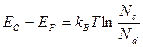 (эВ)
(эВ)
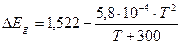
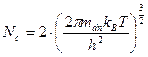 (м-3)
(м-3)
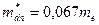
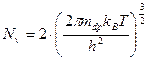 (м-3)
(м-3)

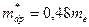
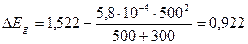 (эВ)
(эВ)
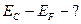
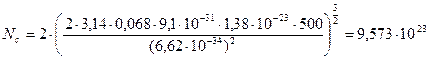 (м-3)
(м-3)
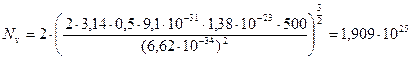 (м-3)
(м-3)
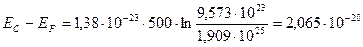 (Дж)
(Дж)
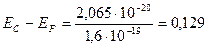 (еВ)
(еВ)
 3. Полупроводник легирован акцепторной примесью до концентрации Na=2ni. Определите, в сколько раз изменится удельная проводимость полупроводника по отношению к собственной, если отношение подвижности электронов и дыр
3. Полупроводник легирован акцепторной примесью до концентрации Na=2ni. Определите, в сколько раз изменится удельная проводимость полупроводника по отношению к собственной, если отношение подвижности электронов и дыр 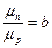 . Считать, что все акцепторы находятся в ионизированом состоянии.
. Считать, что все акцепторы находятся в ионизированом состоянии.
Дано: Решение:
Na=2ni В собственном 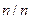 концентрации электронов и дырок
концентрации электронов и дырок
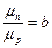 одинаковые
одинаковые 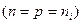

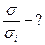
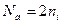
Находим удельную электропроводимость 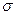
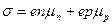
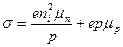 , где
, где 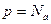 тогда формула получает вид
тогда формула получает вид
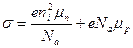
Находим собственную проводимость полупроводника 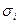
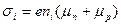 , где
, где 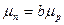 тогда формула получает вид
тогда формула получает вид
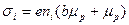
удельная проводимость полупроводника по отношению к собственной:
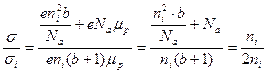
Концентрация нейтральных заряженных акцепторов (доноров) 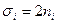 - фактор вырождения примесного уровня.
- фактор вырождения примесного уровня.
4. Образец полупроводника имеет концентрацию доноров Nd=2·1020 м-3. Эффективная масса электрона равняется 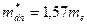 , радиус сферического центра рассеивания донора r=5·10-2 мкм. Определите среднюю длину свободного пробега, среднее время между столкновениями и подвижность электронов при Т=300 К.
, радиус сферического центра рассеивания донора r=5·10-2 мкм. Определите среднюю длину свободного пробега, среднее время между столкновениями и подвижность электронов при Т=300 К.
 Дано: Решение:
Дано: Решение:
Nd=2·1020 м-3 опредиление средней длины свободного пробега λ:
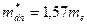
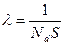
r=5·10-2 мкм площадь находим по формуле: 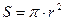
Т=300 К 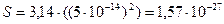 (м-3)
(м-3)

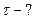 ,
, 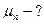
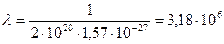
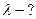 среднее время жизни електронов τ:
среднее время жизни електронов τ:
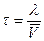 (с)
(с)
для определения обьема кристала 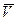 выразим формулу, где
выразим формулу, где 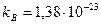 (Дж/к) постоянная.
(Дж/к) постоянная.
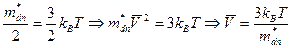
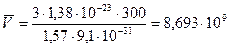
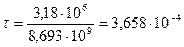 (с)
(с)
подвижность электронов 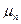 :
:
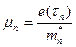
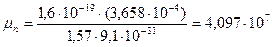 (м2/В·с)
(м2/В·с)
 5. Свет с длиной λ=180 мкм отражается полупроводником с коэффициентом отражения R=0,32. Коэффициент прпускання пленки из такого же материала толщиной h= 1,5 мм представляет Т=0,21. Определите показатель преломления, показатель поглощения и коэффициент поглощения γ.
5. Свет с длиной λ=180 мкм отражается полупроводником с коэффициентом отражения R=0,32. Коэффициент прпускання пленки из такого же материала толщиной h= 1,5 мм представляет Т=0,21. Определите показатель преломления, показатель поглощения и коэффициент поглощения γ.
Дано: Решение:
λ=180 мкм предположим что n>>х, 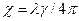 << n.
<< n.
R=0,32 Тогда по известной величине отражения света R с
h= 1,5 мм помощью формулы 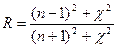 , находим n
, находим n
 Т=0,21
Т=0,21 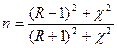
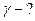 ,
, 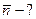 обозначив
обозначив 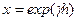 , получаем для х уравнение
, получаем для х уравнение
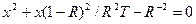
Его решение 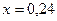 тогда:
тогда:
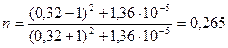
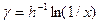 ,
, 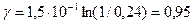 (см-1)
(см-1)
Для света с длиной волны в вакууме l коэффициент пропускання Т (т.е отношение интенсивностей прошедшей и падающей волн) полупро-водниковым cлоем конечной толщины h, помещенным в среду с n=1, выражается:
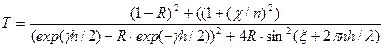 .
.
Фаза x (энергии) определяется формулой
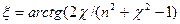 .
.
Синус в знаменателе ответственный за интерференционные эффекты. В их отсутствие – из-за неточной плоскопараллельности поверхностей или из-за немонохрамичности света - имеем
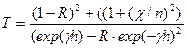 , эту формулу упрощаем
, эту формулу упрощаем
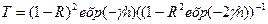
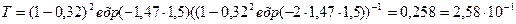
показатель преломления 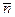 находим по формуле:
находим по формуле:
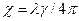 << n
<< n
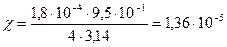
При этом 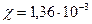 << 1, так что исходное предположение хорошо выполняется.
<< 1, так что исходное предположение хорошо выполняется.
6. Оцените предельную толщину пленки, при которой возможное наблюдение квантово-размерных явлений, если подвижность электронов в пленке 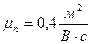 .
.
 Дано: Решение:
Дано: Решение:

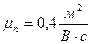
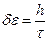
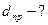
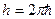
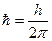 , где
, где 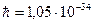 (Дж·с) постоянная Дирака
(Дж·с) постоянная Дирака
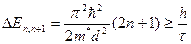
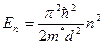
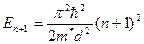
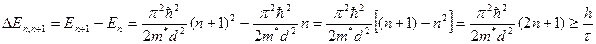
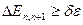
Значение предельной толщины при которой возможное наблюдение квантово-размерных явлений определяется условием:
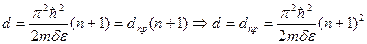
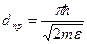 -толщина, при которой дно наинизшей зоны совпадает с заданной энергией
-толщина, при которой дно наинизшей зоны совпадает с заданной энергией 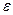 , если
, если 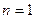
 2015-05-26
2015-05-26 1774
1774