2015-05-26
852
Пусть имеется синусоидальный ток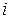 
равный 
.
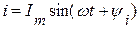На координатной плоскости (рис. 3.4) под углом yi откладываем вектор Im. Проекция вектора на ось ординат дает мгновенное значение этого тока в момент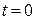 
:
.
 |
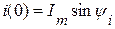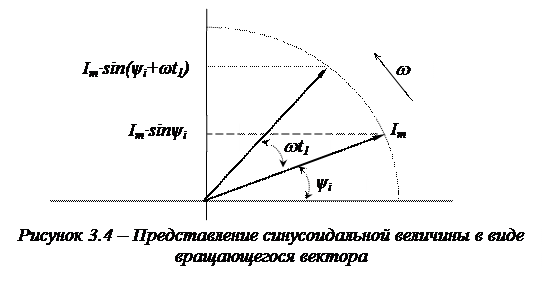Повернем этот вектор против часовой стрелки на некоторый угол равный по величине wt1. Проекция вектора на ось ординат даст значение тока в момент времени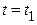 
.
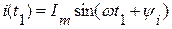Из приведенного выше, следует, что для любого момента времени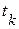 
существует определенное положение вектора 
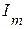, определяемое поворотом против часовой стрелки от оси абсцисс на угол 
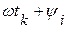. Проекция этого вектора на ось ординат будет давать мгновенное значение синусоидальной величины в момент времени .
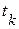Полный оборот вектора произойдет за период времени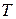 
.
Таким образом, синусоидальную величину можно представить в виде вращающегося вектора с угловой скоростью w против часовой стрелки.
Рассмотрим практическое применение этого положения
Пусть имеются два синусоидальных тока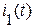 
и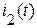 
с одинаковой частотой и различными амплитудами и начальными фазами:
,
.
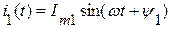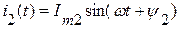Допустим необходимо получить сумму этих токов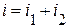 
.
Подобные операции сложения токов синусоидальных величин используются в первом законе Кирхгофа.
В результате сложения этих токов (рис. 3.5), получим синусоидальный ток 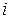такой же частоты, но со своей амплитудой и начальной фазой:
.
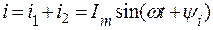Так как частота этих токов одинакова, то они вращаются с одинаковой частотой ω. Т.е. эти вектора друг относительно друга неподвижны, то для определения Im можно применить операцию векторного сложения. В результате такого сложения мы получим величины Im и yi, а следовательно все характеристики мгновенного значения результирующего тока i.
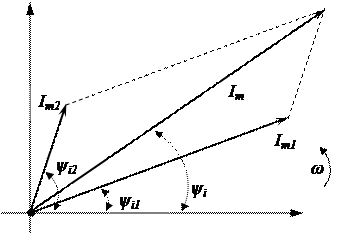
Рисунок 3.5 – Сложение двух векторов
Из примера следует, что законы Кирхгофа для действующих (максимальных) значений цепей синусоидального тока выполняются в векторной форме. Графическое изображение действующих значений токов (напряжений) в электрических схемах называют векторной диаграммой токов (напряжений) цепи.
