Рассмотрим пример электрической цепи, приведенный на рисунке 3.14, состоящей из разнородных элементов (четырех резистивных элементов - 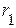 ,
, 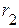 ,
, 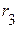 ,
, 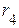 , трех индуктивностей -
, трех индуктивностей - 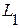 ,
, 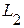 ,
, 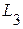 и двух емкостей -
и двух емкостей - 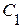 ,
, 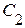 ), соединенных последовательно.
), соединенных последовательно.
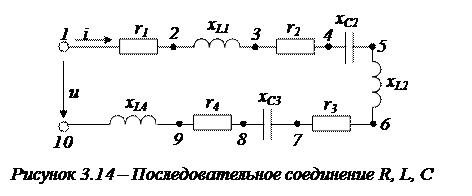
Вычертим векторную диаграмму этой цепи (рис. 3.15).
 |
Вектор тока откладываем в произвольном направлении. Далее откладываем падение напряжения на всех элементах. При этом принимаем во внимание, что напряжения и ток на резистивных элементах совпадают по фазе, напряжение на индуктивных элементах по фазе опережает ток на 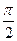 , ток на емкостных элементах опережает напряжение на
, ток на емкостных элементах опережает напряжение на 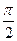 .
.
Используя векторную диаграмму можно определить величину напряжения на любом участке электрической цепи и его сдвиг по фазе относительно тока. Например, напряжение между точками схемы 3 и 8 равно - 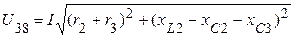 , а между точками 6 и 9 -
, а между точками 6 и 9 - 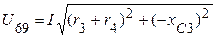 .
.
В общем случае суммарное падение напряжения на резистивных элементах равно 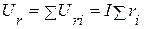 , на индуктивных элементах -
, на индуктивных элементах - 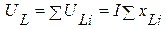 , на емкостных элементах -
, на емкостных элементах - 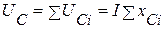 . Таким образом, последовательно соединённые резистивные, индуктивные и емкостные можно заменить эквивалентными. Они соответственно равны:
. Таким образом, последовательно соединённые резистивные, индуктивные и емкостные можно заменить эквивалентными. Они соответственно равны:
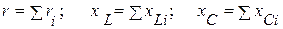 .
.
Тогда полное сопротивление всей ветви, соответственно равно:
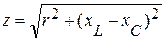
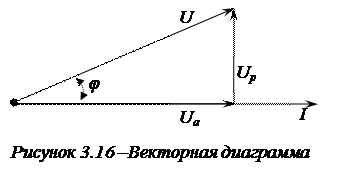 При последовательном соединении резистивного, индуктивного и емкостного элементов, напряжение на зажимах цепи, можно разбить на две составляющие напряжения активную
При последовательном соединении резистивного, индуктивного и емкостного элементов, напряжение на зажимах цепи, можно разбить на две составляющие напряжения активную 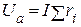 и реактивную
и реактивную 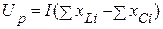 (рис. 3.16).
(рис. 3.16).
В общем случае активная составляющая напряжения равна 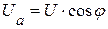 , а реактивная составляющая напряжения –
, а реактивная составляющая напряжения – 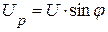 .
.
Возможные варианты расчета цепей с последовательным соединением, рассмотрим на конкретных примерах.
Пример 3.1. В электрической цепи, представленной на рисунке 3.17, заданы величины U = 170 (B), ω = 314 (рад/с) (f = 50 Гц), r1 = 10 (Ом), r2 = 9 (Ом), r3 = 14 (Ом), L1 = 30 (мГн), С2 = 90 (мкФ), L3 = 25 (мГн). Необходимо определить ток в цепи, напряжения на элементах цепи и напряжение на участке 3-6.
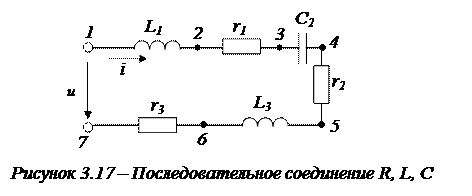 |
1. Определяем омические сопротивления реактивных элементов:
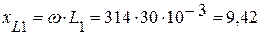 (Ом),
(Ом),
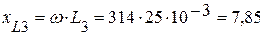 (Ом),
(Ом),
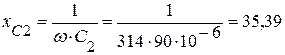 (Ом).
(Ом).
2. Определяем полное сопротивление ветви.
2.1. Эквивалентное активное сопротивление
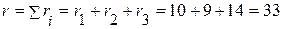 (Ом).
(Ом).
2.2. Эквивалентное индуктивное сопротивление
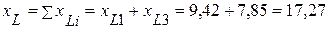 (Ом).
(Ом).
2.3. Эквивалентное емкостное сопротивление
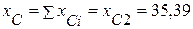 (Ом).
(Ом).
2.4. Полное сопротивление
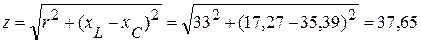 (Ом).
(Ом).
3. Определяем ток в цепи 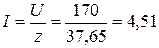 (А).
(А).
4. Определяем напряжения на каждом элементе цепи
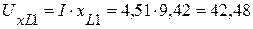 (В),
(В),
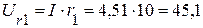 (В),
(В),
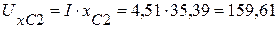 (В),
(В),
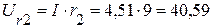 (В),
(В),
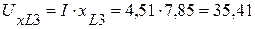 (В),
(В),
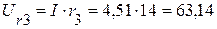 (В).
(В).
5. Напряжение на участке цепи 3-6 равно
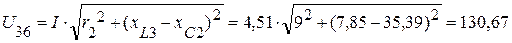 (В).
(В).
6. Векторная диаграмма рассматриваемой цепи приведена на рисун- ке 3.18.
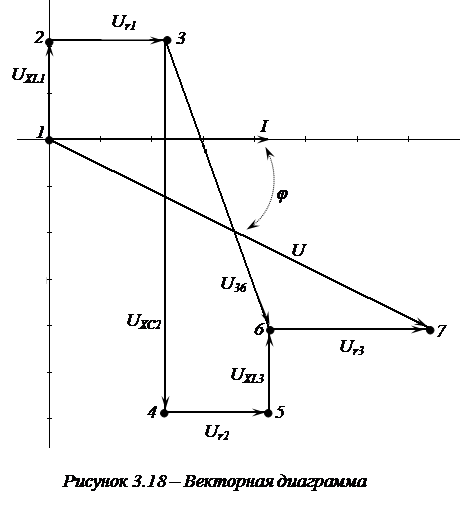 |
Пример 3.2. В электрической цепи, представленной на рисунке 3.19, заданы величины ur1 = 100 (B), ω = 314 (рад/с) (f = 50 Гц), r1 = 20 (Ом), r2 = 15 (Ом), L1 = 50 (мГн), С2 = 100 (мкФ). Необходимо определить ток в цепи, напряжения на элементах цепи и напряжение на участке 2-4.

Рисунок 3.19 – Последовательное соединение R, L, C
1. Определяем омические сопротивления реактивных элементов:
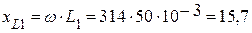 (Ом),
(Ом),
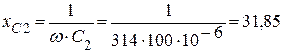 (Ом).
(Ом).
2. Определяем полное сопротивление ветви.
2.1. Эквивалентное активное сопротивление
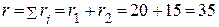 (Ом).
(Ом).
2.2. Полное сопротивление
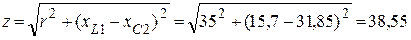 (Ом).
(Ом).
3. Определяем ток в цепи 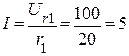 (А).
(А).
4. Определяем напряжения на каждом элементе цепи
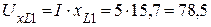 (В),
(В),
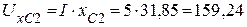 (В),
(В),
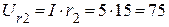 (В).
(В).
5. Определяем напряжение, приложенное к цепи
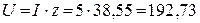 (В).
(В).
6. Напряжение на участке цепи 2-4 равно
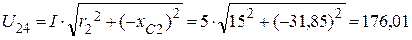 (В).
(В).
 2015-05-26
2015-05-26 1403
1403
