Закон Ома для неоднородного участка цепи

Неоднородный участок цепи показан на рис. 88. Работа всех сил (сто­ронних и электрических), совершаемая при перемещении заряда на участ­ке 1-2, определяется по формуле

dA₁₂ = qε + q (φ₁ – φ₂) (3.91)

По закону сохранения и превращения энергии данная работа dA_l2 равна количеству теплоты dQ, выделяемой на этом участке:

dQ = I²Rdt = IR(Idt) = IRq, (3.92)

т.е. dA₁₂ =dQ или IRq = qε+ q(φ₁ – φ₂), откуда получаем закон Ома для неоднородного участка цепи:

I = 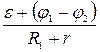(3.93)

где R = R₁ + r —- сопротивление всей цепи, где r — внутреннее сопротив­ление источника, R₁ — сопротивление внешней цепи.

Если участок цепи замкнуть, то φ₁ = φ₂ и уравнение (3.93) запишется

в виде

I = 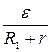(3.94)

Сила тока равна отношению ЭДС, действующей в электрической цепи, к полному сопротивлению цепи.

Уравнение (3.94) называется зако­ном Ома для полной цепи. Различают последовательное и параллельное со­единение источников в батареи.

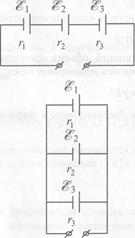
При последовательном соединении п источников (рис. 91,а) ЭДС батареи ε_б равна сумме ЭДС отдельных источ­ников:

ε_б = 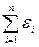(3.95)

Внутреннее сопротивление батареи равно сумме внутренних сопротивле­ний отдельных источников:

R_б = r₁ +r₂ + r₃ = 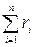(3.96)

а)

б)

Рис. 91

При параллельном соединении источников (рис. 91,б), если соединен­ные элементы имеют одинаковые ЭДС, то ЭДС батареи равна

ε_б = ε₁ = ε₂ =ε₃

Если элементы имеют разные ЭДС, то электрическую цепь можно рассчитывать по правилам Кирхгофа (см. § 84). Сопротивление батареи определяется по формуле

1/R_б = 1/r₁+ 1/r₂+ 1/r₃ (3.97)

Внутреннее сопротивление батареи R₆ из п элементов, имеющих одинаковые внутренние сопротивления г, в n раз меньше, чем сопротив­ление отдельного элемента:

R_б = r/n

Закон Ома для n одинаковых элементов с ЭДС, равной ε, и внутренним

сопротивлением г примет вид:

I = 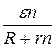- при последовательном соединении и I = 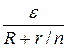— при параллельном соединении источников.

§ 84. Правила Кирхгофа. Расчет разветвленной электрической цепи

Узлом электрической цепи называется точка, в которой сходятся три и бо­лее проводника. В цепи, изображенной на рис. 92, имеется два узла А и В.

Первое правило Кирхгофа ^[2] : алгебраическая сумма токов, сходящихся в узле, равна нулю:

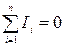(3.98)

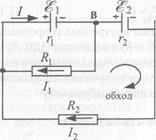
Рис. 92

Токи, притекающие к узлу, считают положительными, а оттекающие от уз­ла — отрицательными. По правилу Кирх­гофа можно записать (k-l) уравнений, где k — число узлов цепи. Произвольно выбирается и обозначается на схеме стрелками направление токов во всех участках цепи (участок — это часть це­пи между соседними узлами).

Для узла А первое правило Кирхгофа запишется в виде

I₁ +I₂ – I = 0 (3.99)

Второе правило Кирхгофа: в любом замкнутом контуре электриче­ской цепи алгебраическая сумма произведений токов на сопротивления соответствующих участков контура равна алгебраической сумме ЭДС, действующих в данном контуре:

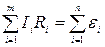(3.100)

где m — число участков, а n —- количество источников в контуре. Число уравнений, записываемых по первому и второму правилам Кирхго­фа, должно быть равно числу токов, текущих в разветвленной цепи.

При применении второго правила Кирхгофа необходимо выполнить следующее:

1) произвольно выбрать и обозначить на схеме направление обхода контура;

2) выделить замкнутые контуры таким образом, чтобы каждый новый контур имел не менее одного участка цепи, не входящего в уже рассмот­ренные контуры;

3) если направление обхода контура совпадает с направлением тока I_i, то произведение I_iR_i - в уравнении (3.100) запишется со знаком плюс, и на­оборот;

4) если направление тока от источника (ток течет по цепи от поло­жительного полюса к отрицательному) совпадает с направлением обхода контура, то соответствующая ЭДС в уравнении (3.100) берется со знаком плюс, и наоборот.

В цепи, изображенной на рис. 92, три замкнутых контура. Применим для двух из них второе правило Кирхгофа (обход контура выбираем по ходу часовой стрелки):

Ir₁ + I₁R₁ = - ε₁ (3.101)

Ir_i+I₂ (R2+r₂) = -ε₁ – ε₂ (3.102)

Допустим, что по условию задачи известны внутренние сопротивления источников r₁ и г₂, сопротивления нагрузки R₁ и R₂ и величины ЭДС ε₁ и ε₂, то, решая уравнения (3.99), (3.101) и (3.102), можно определить токи на уча­стках цепи: I, I₁ и I₂. Если при решении сила тока получилась со знаком ми­нус, то истинное направление тока противоположно выбранному.

§ 85. Электронная проводимость металлов

В начале XX века была создана электронная теория проводимости ме­таллов. Согласно этой теории носителями тока в металлах являются элек­троны проводимости, т. е. электроны, слабосвязанные с ионами кристал­лической решетки металла. Эти электроны между собой не взаимодейст­вуют, а при своем движении сталкиваются с ионами решетки, т. е. элек­троны проводимости ведут себя подобно идеальному одноатомному газу.

В отсутствие внешнего электрического поля электроны проводимости совершают хаотическое тепловое движение со средней квадратичной ско­ростью, зависящей от температуры металла.

Когда к металлу приложено внешнее электрическое поле, то на хаоти­ческое движение электронов накладывается их направленное движение, так называемый дрейф электронов, со средней скоростью, пропорцио­нальной модулю напряженности этого поля. В процессе дрейфа электроны сталкиваются с ионами кристаллической решетки, обусловливая тем са­мым сопротивление проводника электрическому току.

Сопротивление металлических проводников зависит от температуры. При повышении температуры возрастает скорость хаотического теплового движения электронов, увеличивается амплитуда тепловых колебаний по­ложительных ионов в узлах кристаллической решетки. Это приводит к более частым столкновениям электронов с решеткой и к уменьшению ско­рости дрейфа электронов. Чем меньше скорость дрейфа, тем меньший за­ряд переносится через поперечное сечение проводника, тем меньше сила тока в проводнике. А это, согласно закону Ома для участка цепи, свиде­тельствует об увеличении сопротивления проводника.

Пусть при 0°С сопротивление проводника R₀, а при температуре t — R. Опытом установлено, что относительное изменение сопротивления прямо пропорционально изменению температуры:

R = R₀(1 +αt) (3.103)

где α — температурный коэффициент сопротивления, характеризующий за­висимость сопротивления вещества от температуры и численно равный отно­сительному изменению сопротивления проводника при нагревании на 1 К.

Из формулы видно, что размерность [α] = К^-1.

Для химически чистых металлов α = 1/273 K^-1. Существуют сплавы, у

которых температурный коэффициент сопротивления настолько мал, что их сопротивление практически не зависит от температуры. Эти сплавы используют для создания эталонных сопротивлений, шунтов и добавоч­ных сопротивлений к измерительным приборам.

Используя уравнения (3.78) и (3.103), получим формулу, выражаю­щую зависимость удельного сопротивления от температуры:

ρ = ρ₀(1 + αt).

Для чистых металлов при не слишком низких и не слишком высоких температурах а практически не зависит от температуры и температурная зависимость удельного сопротивления является линейной.

У некоторых металлов и сплавов при температурах, близких к абсолют­ному нулю, сопротивление скачком обращается в нуль (рис. 93). Впервые

это явление, названное сверхпроводимостью, было обнаружено в 1911 г. голландским физи­ком Камерлинг-Оннесом^[3] у ртути. Прохождение тока в сверхпроводнике происходит без потерь энергии. Для каждого сверхпроводника имеется своя критическая температура Т_кр, при которой он переходит в сверхпроводящее состояние. Для ртути Т_кр, = 4 К. 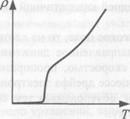Рис. 93

В настоящее время достигнуты значительные успехи в получении высокотемпературной сверхпроводимости. На базе металлокерамики получены вещества, для которых температура пе­рехода в сверхпроводящее состояние Т_кр, превышает температуру сжиже­ния азота (Т_кр = 77 К).

§ 86. Электрический ток в газах.

Самостоятельный и несамостоятельный разряды

В обычных условиях газы являются хорошими изоляторами, т. к. ато­мы и молекулы, из которых они состоят, электрически нейтральны, а кон­центрация носителей тока мала.

Чтобы газ стал проводящим, нужно добиться образования в нем под­вижных заряженных частиц, т. е. ионизировать его. К ионизации газа мо­гут привести его нагревание, воздействие излучений: ультрафиолетового, рентгеновского, радиоактивного.

При ионизации часть атомов газа распадается на положительно заря­женные ионы и электроны. При этом в газе могут образоваться и отрица­тельные ионы вследствие захвата нейтральным атомом свободного элек­трона. После этого газ становится проводящим. Проводимость газов носит ионно-электронный характер.

Наряду с процессом ионизации в газе протекает процесс рекомбина­ции — воссоединения ионов в нейтральные атомы или молекулы. Если внешний ионизатор не будет действовать, проводимость газа уменьшится и газ перестанет быть проводником.

При неизменной мощности ионизатора между процессом ионизации и рекомбинации устанавливается динамическое равновесие, при котором число вновь образующихся пар заряженных частиц равно в среднем числу пар ионов, исчезающих вследствие рекомбинации.

Электрический ток в газах называется газовым разрядом.

Электропроводимость газов, возни­кающая под действием внешнего иониза­тора, называется несамостоятельным га­зовым разрядом.

Предположим, что на воздушный про­межуток между обкладками конденсатора воздействует ультрафиолетовое излучение.

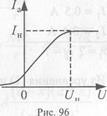
Возникает газовый разряд. Если плавно уве­личивать напряжение на конденсаторе, то сила тока будет увеличиваться до некоторого значения /,„ называемого током насыщения (рис. 94). Возрастание силы тока объясняется тем, что при увеличении напряжения возрастает коли­чество ионов и электронов, движущихся к обкладкам.

При напряжении U„, при котором все образовавшиеся в зазоре заряды достигают обкладок конденсатора, ток максимален при данной интенсив­ности ионизации (ток насыщения). Увеличение напряжения (до значения t/з) не вызовет увеличения тока.

Если источник ионизации перестает действовать, электрический ток через газ прекращается. Описанный процесс — несамостоятельный газовый разряд.

Если после достижения тока насыщения продолжить увеличивать напря­жение (выше t/з), то сила тока резко возрастает. Такой разряд может продол­жаться без внешнего ионизатора. При этом ионы и электроны, необходимые для поддержания электропроводности газа, создаются самим разрядом.

Газовый разряд, который продолжается после прекращения действия внешнего ионизатора, называют самостоятельным газовым разрядом.

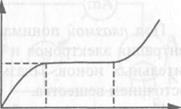U Рис. 94

U_н U_з

Напряжение (Uз, при котором возникает самостоятельный разряд, назы­вают напряжением зажигания газового разряда или напряжением пробоя. Причиной резкого увеличения тока является возрастание числа заряженных частиц за счет ионизации молекул газа при столкновении их с электронами, разогнанными электрическим полем до больших скоростей. При этом кине­тическая энергия электронов оказывается достаточной для того, чтобы они могли совершить работу по отрыву электронов от нейтральных атомов или молекул, т. е. работу ионизации. Произойдет ионизация электронным уда­ром, в результате которой возникает лавина электронов и ионов. Необходи­мость во внешнем ионизаторе для поддержания самостоятельного разряда отпадает. Однако только ионизация электронным ударом не может обеспе­чить длительный самостоятельный разряд. Необходимо, чтобы в газе проте­кал процесс воспроизведения электронов. Если газовый разряд горит между анодом и катодом, то эти электроны испускаются катодом при бомбарди­ровке его положительными ионами, движущимися к катоду под действием электрического поля и вследствие фотоэффекта.

§ 87. Понятие о плазме

Под плазмой понимают сильно ионизированный газ, в котором кон­центрация электронов и отрицательных ионов равна концентрации поло­жительных ионов. Плазма в целом является электрически нейтральным состоянием вещества.

Ионизация газа и образование плазмы могут быть вызваны нагревани­ем газа, а также различными излучениями или бомбардировкой атомов газа быстрыми заряженными частицами. В зависимости от условий сте­пень ионизации плазмы может быть различной. Чем выше температура газа, тем больше ионов и электронов в плазме, тем меньше остается в ней нейтральных молекул.

В зависимости от степени ионизации газа различают частично или полностью ионизованную плазму. Плазма рассматривается как четвертое состояние вещества, т. к. имеет ряд отличительных свойств. Плазма об­ладает хорошей теплопроводностью. Поскольку электроны и ионы плазмы могут перемещаться под действием электрического поля, то по характеру электропроводимости плазма приближается к металлам. В отличие от ме­таллов проводимость плазмы растет с увеличением температуры. При вы­сокой температуре сопротивление плазмы становится исчезающе малым.

Световое излучение плазмы широко используется в лампах дневного света, газоразрядных лампах уличного освещения. Высокая температура плазмы позволяет использовать ее для резки, сварки и плавки металлов. Газоразрядную плазму используют в квантовых источниках света (лазерах).

§ 88. Электрический ток в вакууме.

Электронная эмиссия

Под вакуумом подразумевают такую степень разрежения газа в сосуде, при которой молекулы газа успевают пролететь от одной стенки сосуда к другой, не сталкиваясь друг с другом. Чтобы в вакуумированном баллоне, имеющем два электрода — катод и анод, протекал электрический ток, не­обходим источник заряженных частиц. Действие такого источника осно­вано на свойстве тел испускать электроны. Явление, заключающееся в испускании электронов металлами при сообщении им энергии, необходи­мой для преодоления работы выхода, называется электронной эмиссией. Испускание электронов нагретыми твердыми телами называется термо­электронной эмиссией.

При повышении температуры металла увеличивается кинетическая энергия электронов и часть электронов получает возможность выйти за пределы металла. Получить в вакууме электроны можно и другими спосо­бами, например освещением катодов, изготовленных из щелочных метал­лов. Это так называемая фотоэлектронная эмиссия.

Наконец, с поверхности ме­талла испускаются электроны, когда на нее попадают быстрые заряженные частицы (электроны, ионы и др.). Это вторичная элек­тронная эмиссия.

Все виды эмиссии широко ис­пользуются для получения элек­трического тока в вакууме.

В электронных лампах диодах (двухэлектродная электронная лампа), триодах (трехэлектродная лампа) и т. д. используется явление термоэлек­тронной эмиссии. Если диод включить в цепь (рис. 95), то при накалива­нии нити катода К от батареи накала Б_н и подаче на анод А положительно­го (относительно катода) напряжения от батареи Б_а в лампе возникает электрический ток. Изменяя сопротивление R в цепи, можно получить зависимость анодного тока I _а от анодного напряжения U _a — вольт- амперную характеристику лампы (рис. 96).

Как видно из рис. 96, зависимость тока от на­пряжения не является линейной. В области малых положительных значений напряжений эта зависи­мость описывается законом трех вторых Ленгмюра^[4]:

I = BU^3/2 (3.104)

Здесь В - коэффициент, зависящий от формы, размеров электродов и их взаимного расположе­ния.

При U_a =U_н почти все электроны, вылетающие из катода, достигают анода, наступает ток насыщения. Плотность тока насыщения j_H определя­ется формулой Ричардсона^[5]-Дешмана:

J_н = сТ²е^-А/кТ, (3.105)

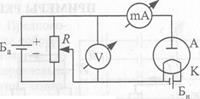
Рис. 95

где А — работа выхода электронов из катода; Т — термодинамическая температура; с — постоянная, одинаковая для всех металлов; к — посто­янная Больцмана.

Явление термоэлектронной эмиссии широко используется в электрон­но-вакуумных приборах и устройствах — электронных лампах, электрон­но-лучевых и рентгеновских трубках, в электронных микроскопах и т. д.

^[1] Эмилий Христианович Лснц (1804-1865) — русский физик и электротехник.

' Ирвинг Ленгмюр (1881-1957) — американский физик.