Эта энергетическая последовательность легко может быть описана при помощи эмпирического правила суммы двух первых квантовых чисел, разработанного в 1951-м годуВ. М. Клечковским и иногда называемого правилом (n + l). Это правило основано на зависимости орбитальной энергии от квантовых чисел n и l и описывает энергетическую последовательность атомных орбиталей как функцию суммы 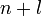 . Суть его очень проста:
. Суть его очень проста:
орбитальная энергия последовательно повышается по мере увеличения суммы 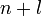 , причём при одном и том же значении этой суммы относительно меньшей энергией обладает атомная орбиталь с меньшим значением главного квантового числа
, причём при одном и том же значении этой суммы относительно меньшей энергией обладает атомная орбиталь с меньшим значением главного квантового числа 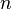 . Например, при
. Например, при 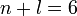 орбитальные энергии подчиняются последовательности
орбитальные энергии подчиняются последовательности 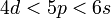 , так как здесь для
, так как здесь для 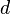 -орбитали главное квантовое число наименьшее
-орбитали главное квантовое число наименьшее 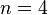 , для
, для  -орбитали
-орбитали 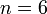 ; наибольшее
; наибольшее 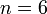 ,
, 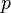 -орбиталь занимает промежуточное положение
-орбиталь занимает промежуточное положение 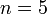 .
.
Или же:
При заполнении орбитальных оболочек атома более предпочтительны (более энергетически выгодны), и, значит, заполняются раньше те состояния, для которых сумма главного квантового числа 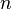 и побочного (орбитального) квантового числа
и побочного (орбитального) квантового числа 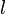 , т.е.
, т.е. 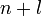 , имеет меньшее значение.
, имеет меньшее значение.
Правило (n + l) в целом хорошо иллюстрирует таблица 1, где по мере постепенного возрастания суммы (n + l) приведена энергетическая последовательность атомных орбиталей. В этой таблице не указаны нереальные (запрещенные квантовой механикой атома) варианты, для которых не выполняется обязательное требование n > l, в частности не указаны комбинации для (n + l)=6:
| n | |||
| l |
| Таблица 1. Энергетическая последовательность орбиталей в изолированных атомах | ||||
| (n + l) | n | l | Атомные орбитали | |
| 1 s | Первый период | |||
| 2 s | Второй период | |||
| 2 p | ||||
| 3 s | Третий период | |||
| 3 p | ||||
| 4 s | Четвёртый период | |||
| 3 d | ||||
| 4 p | ||||
| 5 s | Пятый период | |||
| 4 d | ||||
| 5 p | ||||
| 6 s | Шестой период | |||
| 4 f | ||||
| 5 d | ||||
| 6 p | ||||
| 7 s | Седьмой период | |||
| 5 f | ||||
| 6 d | ||||
| 7 p | ||||
| 8 s | Начало восьмого периода |
Приведённую в таблице очерёдность заполнения электронами атомных орбиталей удобно представить в виде схемы:
 2015-05-30
2015-05-30 9797
9797








