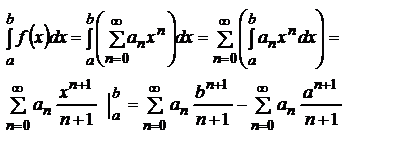
24. Одно замечание о разложении периодической функции в ряд Фурье.
Отметим следующее свойство периодической функции ψ(х) с периодом 2π:
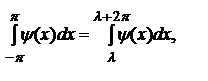 каково бы ни было число λ.
каково бы ни было число λ.
Указанное свойство означает, что интеграл от периодической функции ψ(х) по любому отрезку, длина которого равна периоду, имеет всегда одно и то же значение.
25. Разложение в ряд Фурье четных и нечетных ф-ций на интервале 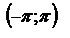 .
.
1. Пусть ф-ция f(x) – четная, т. е. f(-x)=f(x).
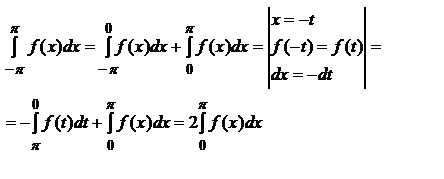
Значит:
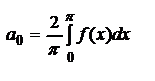 ;
; 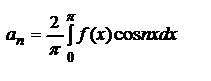 ;
;
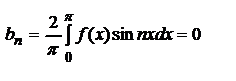 .
.
Ряд Фурье для четных ф-ций – ряд только по косинусам
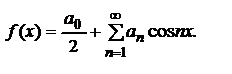
2. Пусть ф-ция f(x) – нечетная, т. е. f(-x)=-f(x).
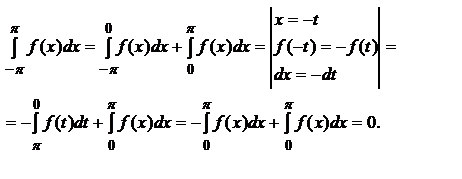
Значит:
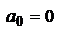 ;
;
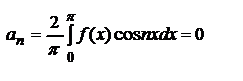 ;
;
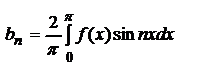 .
.
 2015-05-30
2015-05-30 356
356








