Теорема Абеля

Если степенной ряд сходится при некотором значении 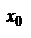, не равном нулю, то он абсолютно сходится при всяком х, для которого .

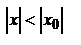Если ряд расходится при некотором значении 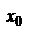, то он расходится при всяком х, для которого .

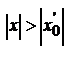Доказательство: Так как по предположению числовой ряд 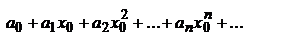сходится, то его общий член 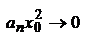при 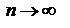, а это значит, что существует такое положительное число М, что все члены ряда по абсолютной величине меньше М. Перепишем ряд в виде 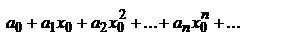и рассмотрим ряд из абсолютных величин его членов:

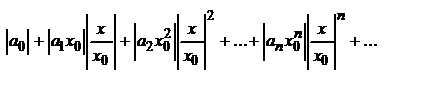Члены этого ряда меньше соответствующих членов ряда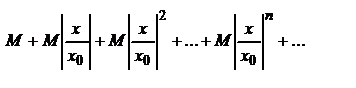

При 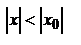последний ряд представляет собой геометрическую прогрессию со знаменателем 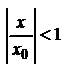и, следовательно, сходится.

Теперь нетрудно доказать и вторую часть теоремы: пусть в некоторой точке 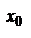ряд расходится. Тогда он будет расходиться в любой точке х, удовлетворяющей условию 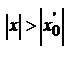. Действительно, если бы в какой-либо точке х-, удовлетворяющей этому условию, ряд сходился, то в силу только что доказанной первой части теоремы он должен был бы сходиться и в точке 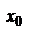, так как 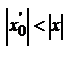. Но это противоречит условию, что в точке 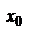ряд расходится. Следовательно, ряд расходится и в точке х. Теорема полностью доказана.