Уравнения движения жидкости

Точные уравнения движения жидкости очень сложны, хотя бы потому, что такие уравнения нелинейные и в частных производных. Тем более, что известные жидкости настолько сильно различаются по физическим свойствам, что и уравнения движения будут для них различными. Это значит, что нельзя написать универсальные уравнения движения, применимые для всех возможных жидкостей.

В целом, жидкости разделяют на две большие группы. Первую из них составляют жидкости Ньютона, для которых связь между касательным напряжением и скоростью задаются в форме

.

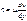Для неньютоновских жидкостей, составляющих вторую группу, такая простая связь не имеет места. Часто для них вязкость является сложной функцией скорости или компонентов тензора напряжений.

Кроме того, есть еще сыпучие среды, которые иногда ведут себя как жидкости, иногда как твердые тела. В определенном смысле их можно отнести к неньютоновским жидкостям.

Теория неньютоновских жидкостей еще далека от совершенства и находится на стадии разработки.

Дальнейшие наши рассуждения относятся к относительно простым жидкостям Ньютона, к которым относится вода, многие водные растворы, ряд распространенных на практике жидкостей (неорганические кислоты, щелочи, солевые растворы), легкие нефтепродукты. Но и в этом случае точные уравнения движения ввиду математической сложности трудно поддаются решению. Поэтому в технических приложениях часто используют упрощенные формы уравнений. Результаты, полученные на основе таких уравнений, зачастую являются грубым приближением. Но они позволяют понять основные черты физических процессов, происходящих в технических устройствах, а на основе численных данных можно с достаточной точностью вести проектные работы.

Уравнение сохранения массы.

Таким уравнением мы явно не пользуемся при решении задач механики материальной точки или твердого тела. Там по умолчанию полагается масса неизменной величиной. В механике сплошных сред закон сохранения массы - это один из фундаментальных законов природы. Рассмотрим трубку тока (рис. 1.4) в установившемся потоке (или, стационарном потоке). Если в трубке тока нет участков с разрывом жидкости, то за равные промежутки времени D t через произвольные сечения S ₁ и S ₂ проходит одинаковая масса m жидкости:

S ₁× v ₁×r₁D t = S ₂× v ₂×r₂D t = m. (1.3)

Если плотность не меняется, то r₁ = r₂ и, вместо (1.3) можем записать

S ₁× v ₁ = S ₂× v ₂. (1.4)

Уравнения (1.3), (1.4) выражают закон сохранения массы.

Уравнение сохранения импульса (энергии).

Пусть имеется струя жидкости, не взаимодействующая с окружающей средой. Такая струя является абстракцией, или идеализацией реальной струи (воды) в воздухе. Плотность воды примерно в тысячу раз больше плотности воздуха, поэтому энергия, передающаяся струей воздуху, очень мала. С хорошей точностью можно считать, струя не взаимодействует с воздухом.

В механике сплошных сред полная энергия D E элемента массы D m, занимающий объем D V и находящийся в поле силы тяжести, определяется как

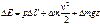. (1.5)

Эта энергия складывается из трех частей. Последние две части нам хорошо знакомы из механики материальной точки - это кинетическая и потенциальная энергия частицы жидкости как целого объекта. Первая же часть p D V - это внутренняя энергия частицы жидкости.

В механике материальной точки она не присутствовала, т.к. там нас не интересовала внутреннее состояние материальной точки, которое молчаливо полагалось неизменным. Хотя ничего не мешало, например, принимать во внимание изменение температуры материального тела за счет работы сил трения. Тогда в записи закона сохранения энергии для материальной точки присутствовала бы еще и внутренняя энергия материальной точки, пропорциональная температуре.

Для невзаимодействующей частицы жидкости ее полная энергия сохраняется, относительно двух произвольных точек 1 и 2 (рис. 1.5) можем записать (D E ₁ = D E ₂)

.

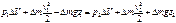Поделив обе части на D V и учитывая определение плотности r = D m /D V, получим

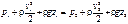. (1.6)

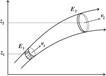
Рис. 1.5.

Вместо (1.6) в литературе используется другая запись

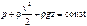. (1.7)

Уравнения (1.6) и (1.7) выражают закон сохранения энергии. Их также можно назвать законом сохранения импульса в интегральной форме, т.к. могут быть получены из уравнения сохранения импульса в дифференциальной форме. Они носят название уравнения Бернулли.

Если жидкость течет по трубе, то она испытывает сильное гидродинамическое сопротивления за счет сил трения, возникающих за счет прилипания молекул жидкости к стенкам трубы. Эти силы сопротивления распределяются по всей области течения, но наибольшее касательное напряжение наблюдается непосредственно вблизи стенки трубы.

Точный расчет силы сопротивления - это довольно сложная задача, особенно там, где имеются геометрически сложные области течения. Но в инженерных расчетах принято пользоваться приближенными формулами.

Работа по преодолению сил сопротивления на локальных участках D A, где имеются геометрические неоднородности (изгибы труб, внезапные сужения или расширения, вентили, клапана и пр.) представляется как

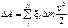, (1.8)

где коэффициенты x _i находятся из опыта, индекс i нумерует тип неоднородностей.

Работа по преодолению сил сопротивления на линейных участках трубопровода D A_l длиной l и диаметром d вычисляется по формуле

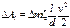, (1.9)

где коэффициент сопротивления z слабо зависит от условия течения и можно полагать равным 0,03.

В случае, когда сопротивление окружающей среды или тел вносит существенный вклад в механику жидкости, то разность полной энергии между точками 1 и 2 равна совершенной работе против сил сопротивления:

D E ₁ - D E ₂ = D A + D A_l. (1.10)

После несложных преобразований, это уравнение можно записать как

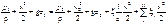. (1.11)