При построении кривой из определенным образом подобранных фрагментов важна не только регулярность самих этих фрагментов, но и выполнение некоторых условий гладкости в точках их состыковки. Только в этом случае составная кривая, получающаяся в результате проведенных построений, будет обладать достаточно хорошими геометрическими характеристиками. Однако при построении составных кривых часто приходится сталкиваться с ситуацией, когда каждый из регулярных фрагментов, участвующих в создании новой кривой, имеет свою собственную параметризацию. Чтобы учесть это обстоятельство, удобно использовать класс так называемых геометрически непрерывных кривых.
Составная кривая называется G1 (геометрически) непрерывной, если вдоль этой кривой единичный вектор ее касательной изменяется непрерывно, и G2-(геометрически) непрерывной, если вдоль этой кривой изменяется непрерывно, кроме того, и вектор кривизны. Обратимся к рассмотрению составных кривых Безье. Составная кубическая кривая Безье представляет собой объединение элементарных кубических кривых Безье g1...gm, таких, что
ri(1) = ri+1(0), i = 0,..., m-1,
где r = ri(t), 0 £ t £ 1 - параметрическое уравнение кривой gi.
Чтобы составная кривая Безье, определяемая набором вершин V0,V1,...,Vm-1, Vm,
1) была G1-непрерывной кривой, необходимо, чтобы каждые три точки V3i-1,V3i, V3i+1 этого набора лежали на одной прямой;
2) была замкнутой G1-непрерывной кривой, необходимо, кроме того, чтобы совпадали первая и последняя точки, V0=Vm, и три точки Vm-1, Vm = V0, V1 лежали на одной прямой;
3) была G2-непрерывной кривой, необходимо, чтобы каждые пять точек V3i-2, V3i-2, V3i, V3i+1, V3i+2 (i ³ 1) заданного набора лежали в одной плоскости.
Попытаемся найти другой класс кривых, сохраняющих перечисленные достоинства кривых Безье и лишенных их недостатков. Так как в векторном уравнении, задающем кривую Безье, векторные составляющие постоянны (это просто вершины массива), то мы уделим основное внимание выбору новых функциональных коэффициентов, стараясь (разумеется, по возможности) сохранить при этом замечательные свойства многочленов Бернштейна, ограничив наши рассмотрения кубическими многочленами.
По заданному набору точек V0,V1,V2,V3 элементарная кубическая В-сплайновая кривая определяется при помощи векторного параметрического уравнения следующего вида:
r(t) = [(1-t)3×V0 + (3t3 - 6t2 + 4)×V1 + (-3t3 + 3t2 +3t +1)×V2 + t3×V3]/6, 0 £ t £ 1
или, в матричной форме, r(t)=VMT, 0 £ t £ 1
где 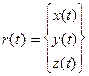 V= (V0 V1 V2 V3) =
V= (V0 V1 V2 V3) = 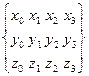
M = 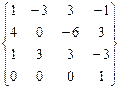 , T =
, T = 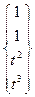
Матрица М называется базисной матрицей В-сплайновой кривой.
Функциональные коэффициенты в уравнении, определяющем элементарную В-сплайновую кубическую кривую, неотрицательны, в сумме составляют единицу, универсальны (не зависят от конкретного вида точек в заданной четверке).
Это означает, что рассматриваемый элементарный фрагмент лежит внутри выпуклой оболочки заданных вершин - четырехугольника (в плоском случае) или тетраэдра (в пространственном случае) (рис. 13).
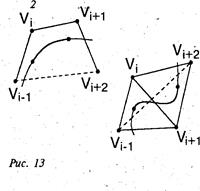
Составная кубическая В-сплайновая кривая, задаваемая параметрическим уравнением
r = r(t), 0 £. t £. т - 2,
и определяемая набором точек
V0, V1;..,Vm-1, Vm, (m ³ 3),
представляет собой объединение m-2 элементарных кубических В-сплайновых кривых, g3,..., gm, описываемых уравнениями вида
r = ri(t) = (Vi-1 Vi Vi+1 Vi+2) M 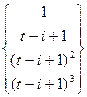 i-1 £ t £ i i = 1,....., m-2
i-1 £ t £ i i = 1,....., m-2
 2015-05-30
2015-05-30 586
586








