А. Случай одной переменной
Обратимся для определенности к задаче интерполяции и начнем рассмотрение с обсуждения правил выбора класса кривых,
Ясно, что допустимый класс кривых должен быть таким, чтобы решение задачи было единственным (это обстоятельство сильно помогает в преодолении многих трудностей поиска). Кроме того, желательно, чтобы построенная кривая изменялась плавно.
Пусть на плоскости задан набор точек (хi, уi), i = 0, 1,..., m,
таких, что x0 < x1<..,<xm-1 < хm.
То обстоятельство, что точки заданного набора занумерованы в порядке возрастания их абсцисс, позволяет искать кривую в классе графиков функций. Мы сможем описать основные проблемы сглаживания этого дискретного набора, ограничившись случаем многочленов. Как известно из курса математического анализа, существует интерполяционный многочлен Лагранжа
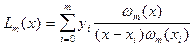 ,
,
где 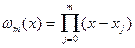 ,
,
график которого проходит через все заданные точки (хi, уi), i = 0, 1,..., m,
Это обстоятельство и простота описания (заметим, что многочлен однозначно определяется набором своих коэффициентов; в данном случае их число совпадает с количеством точек в заданном наборе) являются несомненными достоинствами построенного интерполяционного многочлена (разумеется, есть и другие).
Однако нам полезно остановиться и на некоторых недостатках предложенного подхода.
1. Степень многочлена Лагранжа на единицу меньше числа заданных точек. Поэтому, чем больше точек задано, тем выше степень такого многочлена. И хотя график интерполяционного многочлена Лагранжа всегда будет проходить через все точки массива, его уклонение (от ожидаемого) может оказаться довольно значительным (рис. 2).
2. Изменение одной точки (ситуация, довольно часто встречаемая на практике) требует полного пересчета коэффициентов интерполяционного многочлена и к тому же может существенно повлиять на вид задаваемой им кривой.
Приближающую кривую можно построить и совсем просто: если последовательно соединить точки заданного набора прямолинейными отрезками, то в результате получится ломаная (рис.3). При такой, кусочно-линейной, интерполяции требуется найти всего 2m чисел (каждый прямолинейный отрезок определяется ровно двумя коэффициентами), но, к сожалению, построенная таким образом, аппроксимирующая кусочно-линейная функция не обладает нужной гладкостью: уже первая производная этой функции терпит разрывы в узлах интерполяции.
Рассмотрев эти две крайние ситуации, попробуем найти класс функций, которые в основном сохранили бы перечисленные выше достоинства обоих подходов и одновременно были бы в известной степени свободны от их недостатков.
Для этого поступим так: будем использовать многочлены (как и в первом случае) и строить их последовательно, звено за звеном (как во втором случае). В результате получится так называемый полиномиальный многозвенник. При подобном подходе важно правильно выбрать степени привлекаемых многочленов, а для плавного изменения результирующей кривой необходимо еще тщательно подобрать коэффициенты многочленов (из условий гладкого сопряжения соседних звеньев).
То, что получится в результате описанных усилий, называют сплайн-функциями или просто сплайнами.
Для того чтобы понять, какое отношение имеют сплайн-функции к чертежным сплайнам, возьмем гибкую стальную линейку, поставим ее на ребро и, закрепив один из концов в заданной точке, поместим ее между опорами, которые располагаются в плоскости Оху в точках (хi, уi), i = 0, 1,..., m, где x0 < x1<..,<xm-1 < хm (рис.4).
Интересно отметить, что функция y=S(x), описывающая профиль линейки, обладает следующими интересными свойствами:
• с довольно большой точностью часть графика этой функции, заключенную между любыми двумя соседними опорами, можно считать многочленом третьей степени;
• на всем промежутке [x0, xm] функция у = S(x) дважды непрерывно дифференцируема.
Построенная функция S(x) относится к так называемым интерполяционным кубическим сплайнам. Этот класс в полной мере удовлетворяет высказанным выше требованиям и обладает еще целым рядом замечательных свойств.
Перейдем, однако, к точным формулировкам.
Интерполяционным кубическим сплайном называется функция S(x), обладающая следующими свойствами:
1) график этой функции проходит через каждую точку заданного массива,
S(xi) = yi,i = 0,l,...,m;
2) на каждом из отрезков [хi, xi-1], i = 0, 1,..., m-1, функция является многочленом третьей степени,
S(x) = 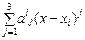
3) на всем отрезке задания [x0, xm] функция S(x) имеет непрерывную вторую производную.
Так как на каждом из отрезков [хi, xi+1], сплайн S(x) определяется четырьмя коэффициентами, то для его полного построения на всем отрезке задания необходимо найти 4m чисел.
Третье условие будет выполнено, если потребовать непрерывности сплайна во всех внутренних узлах хi, i=l,..., m-1 (это дает m-1 условий на коэффициенты), а также его первой (m-1 условий) и второй (еще m-1 условий) производных в этих узлах. Вместе с первым условием получаем m-1 + m-1 + m-1 + m+1 = 4m - 2 равенства. Недостающие два условия для полного определения коэффициентов можно получить, задав, например, значения первых производных на концах отрезка [x0, xm] (граничные условия):
S'(x0)=l0, S'(xm)=lm
Существуют граничные условия и других типов.
Б. Случай двух переменных
Более сложная задача построения по заданному набору точек в трехмерном пространстве интерполяционной функции двух переменных решается, похожим образом.
Расскажем, прежде всего, что такое интерполяционный бикубический сплайн.
Пусть на плоскости задан набор из (m+l)(n+l) точек (рис. 5)
(xi,yj), i=0,l,...,m; j=0,l,...,n,
где x0<x1,...<xm-1<хm; у0 <y1 <...<yn-1 <yn.
Добавим к каждой паре (хi, уj третью координату zij - (х,, yj, zij).
Тем самым мы получаем массив
(х,, yj, zij) i=0,l,...,m; j=0,l,...,n,
Прежде чем строить поверхность, проходящую через все точки заданного массива, определим функцию, отображением которой будет эта поверхность.
Интерполяционным бикубическим сплайном называется функция двух переменных S(x, у), обладающая следующими свойствами:
1) эта функция проходит через каждую точку заданного массива,
S(xi,yj)=zij i=0, l,..., m; j=0, l,...,n;
2) на каждом частичном прямоугольнике
[хi, xi+1] ´ [yj, yj+1], i =0, 1,..., m-1, j = 0, 1,..., n-l;
функция представляет собой многочлен третьей степени по каждой из переменных;
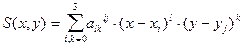 ;
;
3) на всем прямоугольнике задания [х0, хm,]´[у0,.yn] функция S(х, у) имеет по каждой переменной непрерывную вторую производную.
Для того чтобы построить по заданному массиву {(хi, уj, zij.)} интерполяционный бикубический сплайн, достаточно определить все 16mn коэффициентов. Как и в одномерном случае, отыскание коэффициентов сплайн-функции сводится к построению решения системы линейных уравнений, связывающих искомые коэффициенты alkij. Последняя возникает из первого и третьего условий; после добавления к ним недостающих соотношений путем задания значений 1 производной искомой функции в граничных узлах прямоугольника [х0, хm,]´[у0,.yn] или иных соображений.
Подведем некоторые итоги.
Достоинства предложенного способа несомненны. Для решения линейных систем, возникающих в ходе построения сплайн-функций, существует много эффективных методов, к тому же эти системы достаточно просты. Сплайн-функции проходят через все заданные точки, полностью сохраняя первоначально заданную информацию.
Вместе с тем изменение лишь одной точки (случай на практике довольно типичный) при описанном подходе заставляет пересчитывать заново, как правило, все коэффициенты alkij. К тому же во многих задачах исходный набор точек задается приближенно и, значит, требование неукоснительного прохождения графика искомой функции через каждую точку этого набора оказывается излишним.
От этих недостатков свободны некоторые из методов сглаживания, к описанию которых мы и переходим. Но прежде всего мы значительно расширим классы, в которых будет вестись поиск соответствующих кривых и поверхностей. Более точно, мы откажемся от требования однозначного проектирования искомой кривой на координатную ось, а поверхности - на координатную плоскость. Такой подход позволяет ослабить и требования к задаваемому массиву.
Сказанное требует небольшого геометрического введения.
Начнем, как и прежде, с кривых.
Сплайновые кривые
Нам будет удобно пользоваться параметрическими уравнениями кривой. Напомним необходимые понятия.
Параметрически заданной кривой называется множество g точек М (х, у, z), координаты х, у, z которых определяются соотношениями
x = x(t), у = y(t), z = z(t), (1)
a < t < b,
где x(t), y(t),z(t) - функции, непрерывные на отрезке [а, b] (рис. 6).
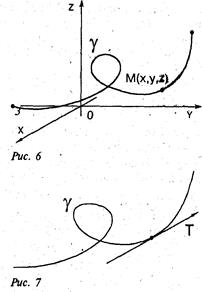
Соотношения (1) называются параметрическими уравнениями кривой g.
Без ограничения общности можно считать, что а = 0 и b = 1; этого всегда можно добиться при помощи замены вида
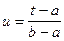
Полезна векторная форма записи параметрических уравнений r =r (t), 0< t < 1,
где r(t) = (x(t), y(t), z(t)).
Параметр t задает ориентацию параметризованной кривой g (порядок прохождения точек при монотонном возрастании параметра).
Кривая g называется регулярной кривой, если r’(t) ¹ 0 в каждой ее точке. Это означает, что в каждой точке кривой существует касательная к ней и эта касательная меняется непрерывно вслед за перемещающейся вдоль кривой ее текущей точки (рис. 7). Единичный вектор касательной к кривой у равен
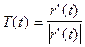
Если дополнительно потребовать, чтобы задающая кривую векторная функция имела вторую производную, то будет определен вектор кривизны кривой
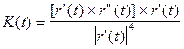 ,
,
модуль которого характеризует степень ее отклонения от прямой (рис. 8). В частности, если g - отрезок прямой, то К = 0.
 2015-05-30
2015-05-30 1676
1676