Введение в математический анализ
1.1. Определение и свойства предела последовательности.
Числовая последовательность.
Если каждому натуральному числу  поставлено в соответствие число
поставлено в соответствие число  , то говорят, что задана последовательность:
, то говорят, что задана последовательность: 
Общий элемент последовательности является функцией от  :
: 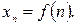
Таким образом, последовательность может рассматриваться как функция порядкового номера элемента.
Задать последовательность можно различными способами – главное, чтобы был указан способ получения любого члена последовательности.
Пример 1.  или
или 
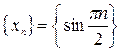 или
или 
Для последовательностей можно определить следующие операции:
1) умножение последовательности на число  :
: 
 , т.е.
, т.е. 
2) сложение (вычитание) последовательностей:  ;
;
3) произведение последовательностей:  ;
;
4) частное последовательностей:  при
при 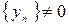 .
.
Ограниченные и неограниченные последовательности.
Последовательность  называется ограниченной, если существует такое число
называется ограниченной, если существует такое число  , что для любого n верно неравенство:
, что для любого n верно неравенство:  т.е. все члены последовательности принадлежат промежутку
т.е. все члены последовательности принадлежат промежутку  .
.
Последовательность  называется ограниченной сверху, если для любого
называется ограниченной сверху, если для любого  существует такое число
существует такое число  , что:
, что:  .
.
Последовательность  называется ограниченной снизу, если для любого
называется ограниченной снизу, если для любого  существует такое число
существует такое число  , что:
, что:  .
.
Пример 2.  – ограничена снизу
– ограничена снизу  .
.
Число  называется пределом последовательности
называется пределом последовательности  , если для любого положительного
, если для любого положительного 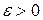 существует такой номер
существует такой номер  , что для всех
, что для всех  выполняется условие:
выполняется условие: 
Это записывается:  .
.
В этом случае говорят, что последовательность  сходится к
сходится к  при
при  .
.
Свойство: если отбросить какое-либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.
Пример 3. Доказать, что предел последовательности  .
.
Пусть при  верно
верно  , т.е.
, т.е.  . Это верно при
. Это верно при  , таким образом, если за
, таким образом, если за  взять целую часть от
взять целую часть от  , то утверждение, приведенное выше, выполняется.
, то утверждение, приведенное выше, выполняется.
Пример 4. Показать, что при  последовательность
последовательность  имеет пределом число
имеет пределом число  .
.
Итого:  .
.
Очевидно, что существует такое число  , что
, что  , т.е.
, т.е. 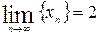 .
.
Теорема 1. Последовательность не может иметь более одного предела.
Доказательство. Предположим, что последовательность  имеет два предела
имеет два предела  и
и  , не равные друг другу:
, не равные друг другу:  ;
;  ;
;  .
.
Тогда по определению существует такое число 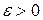 , что
, что

Запишем выражение:

А т.к. 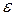 - любое число, то
- любое число, то 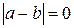 , т.е.
, т.е. 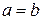 .
.
Теорема 2. Если  , то
, то  .
.
Доказательство. Из  следует, что
следует, что  . В то же время:
. В то же время:
 , т.е.
, т.е. 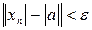 , т.е.
, т.е.  .
.
Теорема 3. Если  , то последовательность
, то последовательность  ограничена.
ограничена.
Следует отметить, что обратное утверждение неверно, т.е. из ограниченности последовательности не следует ее сходимость.
Например, последовательность  не имеет предела, хотя
не имеет предела, хотя 
Монотонные последовательности.
1) Если  для всех
для всех  , то последовательность возрастающая.
, то последовательность возрастающая.
2) Если  для всех
для всех  , то последовательность неубывающая.
, то последовательность неубывающая.
3) Если 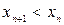 для всех
для всех  , то последовательность убывающая.
, то последовательность убывающая.
4)Если  для всех
для всех  , то последовательность невозрастающая
, то последовательность невозрастающая
Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными.
Пример 5.  – убывающая и ограниченная
– убывающая и ограниченная  – возрастающая и неограниченная.
– возрастающая и неограниченная.
Пример 6. Доказать, что последовательность 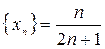 монотонная возрастающая.
монотонная возрастающая.
Найдем член последовательности 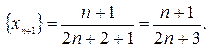
Найдем знак разности:
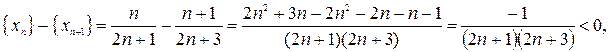 т.к.
т.к. 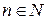 , то знаменатель положительный при любом
, то знаменатель положительный при любом  .
.
Таким образом,  . Последовательность возрастающая, что и следовало доказать.
. Последовательность возрастающая, что и следовало доказать.
Пример 7. Выяснить, является возрастающей или убывающей последовательность: 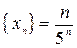 .
.
Найдем  . Найдем разность
. Найдем разность 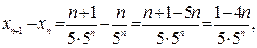
т.к. 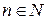 , то
, то 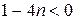 , т.е.
, т.е. 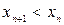 . Последовательность монотонно убывает.
. Последовательность монотонно убывает.
Следует отметить, что монотонные последовательности ограничены по крайней мере с одной стороны.
Теорема 4. Монотонная ограниченная последовательность имеет предел.
Доказательство. Рассмотрим монотонную неубывающую последовательность

Эта последовательность ограничена сверху:  , где
, где  – некоторое число.
– некоторое число.
Т.к. любое, ограниченное сверху, числовое множество имеет четкую верхнюю грань, то для любого 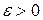 существует такое число
существует такое число  , что
, что  , где
, где  – некоторая верхняя грань множества.
– некоторая верхняя грань множества.
Т.к.  - неубывающая последовательность, то при
- неубывающая последовательность, то при 
 ,
,  .
.
Отсюда 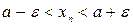 ,
,  или
или  , т.е.
, т.е. 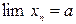 .
.
Для остальных монотонных последовательностей доказательство аналогично.
Число  .
.
Рассмотрим последовательность 
Если последовательность  монотонная и ограниченная, то она имеет конечный предел.
монотонная и ограниченная, то она имеет конечный предел.
По формуле бинома Ньютона:
 или, что то же самое
или, что то же самое

Покажем, что последовательность  – возрастающая. Действительно, запишем выражение
– возрастающая. Действительно, запишем выражение 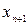 и сравним его с выражением
и сравним его с выражением  :
:
 Каждое слагаемое в выражении
Каждое слагаемое в выражении 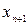 больше соответствующего значения
больше соответствующего значения  , и, кроме того, у
, и, кроме того, у 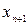 добавляется еще одно положительное слагаемое. Таким образом, последовательность
добавляется еще одно положительное слагаемое. Таким образом, последовательность  возрастающая.
возрастающая.
Докажем теперь, что при любом n ее члены не превосходят трех:  .
.
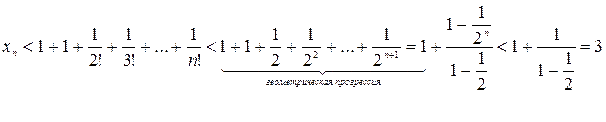
Итак, последовательность  - монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой
- монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой  :
: 
Из неравенства  следует, что
следует, что  . Отбрасывая в равенстве для
. Отбрасывая в равенстве для  все члены, начиная с четвертого, имеем:
все члены, начиная с четвертого, имеем:

переходя к пределу, получаем: 
Таким образом, число е заключено между числами 2,5 и 3. Если взять большее количество членов ряда, то можно получить более точную оценку значения числа 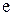 . Можно показать, что число
. Можно показать, что число 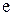 иррациональное и его значение равно 2,71828…
иррациональное и его значение равно 2,71828…
Аналогично можно показать, что  , расширив требования к х до любого действительного числа.
, расширив требования к х до любого действительного числа.
Предположим, что:  , тогда
, тогда 

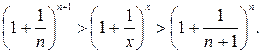
Найдем 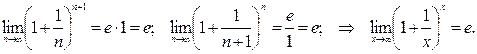
Число  является основанием натурального логарифма.
является основанием натурального логарифма.



Выше представлен график функции 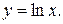
Связь натурального и десятичного логарифмов.
Пусть 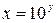 , тогда
, тогда 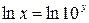 , следовательно
, следовательно 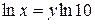 .
.
 ,
,
где  - модуль переход.
- модуль переход.
1.2 Определение и свойства предела функции.
Предел функции в точке.
 y f(x)
y f(x)
A+e
A
A-e
0 a-D а a+D x
Пусть функция 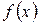 определена в некоторой окрестности точки
определена в некоторой окрестности точки  (т.е. в самой точке
(т.е. в самой точке  функция может быть и не определена).
функция может быть и не определена).
Число  называется пределом функции
называется пределом функции 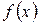 при
при  , если для любого
, если для любого 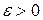 существует такое число
существует такое число 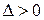 , что для всех
, что для всех 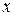 таких, что:
таких, что:  верно неравенство
верно неравенство  .
.
То же определение может быть записано в другом виде:
если 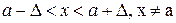 , то верно неравенство
, то верно неравенство 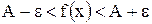 .
.
Запись предела функции в точке: 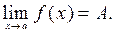
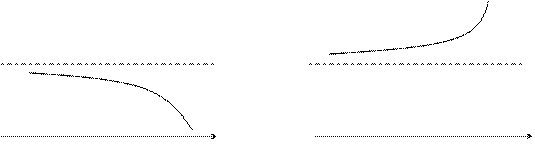
Предел функции при стремлении аргумента к бесконечности.
Число  называется пределом функции
называется пределом функции 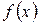 при
при  , если для любого числа
, если для любого числа 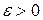 существует такое число
существует такое число  , что для всех
, что для всех 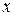 ,
, 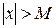 выполняется неравенство:
выполняется неравенство: 
При этом предполагается, что функция 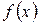 определена в окрестности бесконечности.
определена в окрестности бесконечности.
Записывают: 
Графически можно представить:
 y y
y y
A A
0 0
x x

 y y
y y
 |
A
A
0 x 0 x
Аналогично можно определить пределы  для любого
для любого 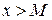 и
и 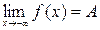 для любого
для любого  .
.
Основные теоремы о пределах.
Теорема 1.  , где
, где 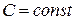 .
.
Следующие теоремы справедливы при предположении, что функции  и
и  имеют конечные пределы при
имеют конечные пределы при  .
.
Теорема 2. 
Доказательство этой теоремы будет приведено ниже.
Теорема 3. 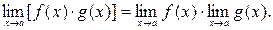
Следствие. 
Теорема 4.  при
при 
Теорема 5. Если 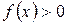 вблизи точки
вблизи точки  и
и  , то
, то  .
.
Аналогично определяется знак предела при  ,
,  ,
,  .
.
Теорема 6. Если 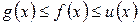 вблизи точки
вблизи точки  и
и 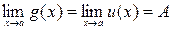 , то и
, то и  .
.
Функция 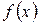 называется ограниченной вблизи точки
называется ограниченной вблизи точки  , если существует такое число
, если существует такое число 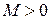 , что
, что  вблизи точки
вблизи точки  .
.
Теорема 7. Если функция 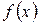 имеет конечный предел при
имеет конечный предел при  , то она ограничена вблизи точки
, то она ограничена вблизи точки  .
.
Доказательство. Пусть  , т.е.
, т.е.  , тогда
, тогда 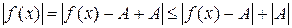 или
или  , т.е.
, т.е. 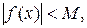 где
где 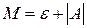 .
.
1.3. Замечательные пределы. Применение эквивалентных бесконечно малых величин к вычислению пределов.
Некоторые замечательные пределы.
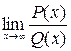 , где
, где  ,
,  - многочлены.
- многочлены.

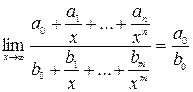
 Итого:
Итого: 
 Первый замечательный предел:
Первый замечательный предел: 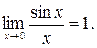

Второй замечательный предел: 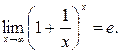
Часто, если непосредственное нахождение предела какой–либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.
Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения:


Пример 8. Найти предел 

Пример 9. Найти предел 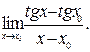

Пример 10. Найти предел 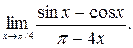

Пример 11. Найти предел 

Пример 12. Найти предел.
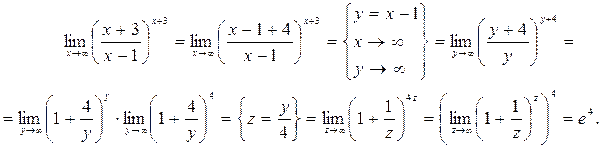 Пример 13. Найти предел
Пример 13. Найти предел  .
.
Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби:

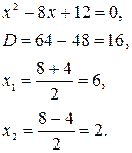
Тогда 
Пример 14. Найти предел 
Домножим числитель и знаменатель дроби на сопряженное выражение: 
Пример 15. Найти предел 

Пример 16. Найти предел  .
.
Разложим числитель и знаменатель на множители:

тогда 
Пример 17. Найти предел 

Функция 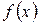 называется бесконечно малой при
называется бесконечно малой при  , где
, где  может быть числом или одной из величин ¥, +¥ или -¥, если
может быть числом или одной из величин ¥, +¥ или -¥, если 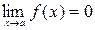 .
.
Бесконечно малой функция может быть только если указать, к какому значению  стремится аргумент
стремится аргумент 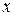 . При различных значениях
. При различных значениях  функция может быть бесконечно малой или нет.
функция может быть бесконечно малой или нет.
Пример 18. Функция 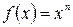 является бесконечно малой при
является бесконечно малой при  и не является бесконечно малой при
и не является бесконечно малой при  , т.к.
, т.к.  .
.
Теорема 8. Для того, чтобы функция 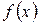 при
при  имела предел, равный
имела предел, равный  , необходимо и достаточно, чтобы вблизи точки
, необходимо и достаточно, чтобы вблизи точки  выполнялось условие:
выполнялось условие:  , где
, где 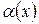 – бесконечно малая при
– бесконечно малая при  (
(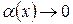 при
при  ).
).
Свойства бесконечно малых функций:
1. Сумма фиксированного числа бесконечно малых функций при  тоже бесконечно малая функция при
тоже бесконечно малая функция при  .
.
2. Произведение фиксированного числа бесконечно малых функций при  тоже бесконечно малая функция при
тоже бесконечно малая функция при  .
.
3. Произведение бесконечно малой функции на функцию, ограниченную вблизи точки  , является бесконечно малой функцией при
, является бесконечно малой функцией при  .
.
4. Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю, есть величина бесконечно малая.
Используя понятие бесконечно малых функций, приведем доказательство некоторых теорем о пределах, приведенных выше.
Доказательство свойства 2.
Представим  , где
, где 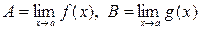 , тогда
, тогда  ,
,  ,
, 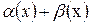 – бесконечно малая, значит
– бесконечно малая, значит 
Доказательство свойства 3.
Представим  , где
, где 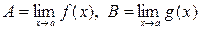 , тогда
, тогда 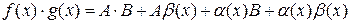 ,
,  ,
,  – бесконечно малые, значит
– бесконечно малые, значит 
 2015-05-30
2015-05-30 4069
4069







