Предел функции 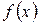 при
при  , где
, где  - число, равен бесконечности, если для любого числа
- число, равен бесконечности, если для любого числа  существует такое число
существует такое число 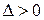 , что неравенство:
, что неравенство: 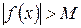 выполняется при всех
выполняется при всех 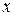 , удовлетворяющих условию:
, удовлетворяющих условию:  .
.
Записывается  .
.
Собственно, если в приведенном выше определении заменить условие 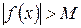 на
на  то получим:
то получим: 
а если заменить на  то
то 
Графически приведенные выше случаи можно проиллюстрировать следующим образом:
 |
a x a x a x
Функция называется бесконечно большой при  , где
, где  – число или одна из величин
– число или одна из величин  ,
,  или
или  , если
, если  , где
, где  – число или одна из величин
– число или одна из величин  ,
,  или
или  .
.
Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.
Теорема 9. Если  при
при  (или
(или  ) и не обращается в ноль, то
) и не обращается в ноль, то 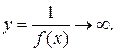
Сравнение бесконечно малых функций.
Пусть  – бесконечно малые функции при
– бесконечно малые функции при  . Будем обозначать эти функции
. Будем обозначать эти функции 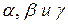 соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.
соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.
Например, функция  стремится к нулю быстрее, чем функция
стремится к нулю быстрее, чем функция 
Если  , то функция
, то функция  называется бесконечно малой более высокого порядка, чем функция
называется бесконечно малой более высокого порядка, чем функция 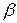 .
.
|
|
|
Если 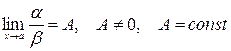 , то
, то  называются бесконечно малыми одного порядка.
называются бесконечно малыми одного порядка.
Если  то функции
то функции  называются эквивалентными бесконечно малыми. Записывают
называются эквивалентными бесконечно малыми. Записывают  ~
~ 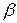 .
.
Пример 19. Сравним бесконечно малые при  функции
функции  и
и 
 т.е. функция
т.е. функция  – бесконечно малая более высокого порядка, чем
– бесконечно малая более высокого порядка, чем 
Бесконечно малая функция  называется бесконечно малой порядка
называется бесконечно малой порядка  относительно бесконечно малой функции
относительно бесконечно малой функции 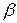 , если предел
, если предел 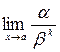 конечен и отличен от нуля.
конечен и отличен от нуля.
Однако следует отметить, что не все бесконечно малые функции можно сравнивать между собой. Например, если отношение 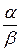 не имеет предела, то функции несравнимы.
не имеет предела, то функции несравнимы.
Пример 20. Если 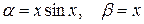 , то при
, то при 
 , т.е. функция
, т.е. функция  - бесконечно малая порядка 2 относительно функции
- бесконечно малая порядка 2 относительно функции 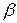 .
.
Пример 21. Если 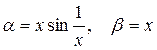 , то при
, то при 
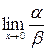 не существует, т.е. функция
не существует, т.е. функция  не сравнимы.
не сравнимы.
Свойства эквивалентных бесконечно малых.
1)  ~
~  ,
, 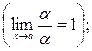
2) если  ~
~ 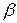 и
и 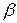 ~
~  , то
, то  ~
~  ,
, 
3) если  ~
~ 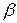 , то
, то 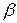 ~
~  ,
, 
4) если  ~
~ 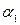 и
и 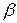 ~
~  и
и  , то и
, то и  или
или  .
.
Следствие: а) если  ~
~ 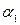 и
и  , то и
, то и 
б) если 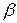 ~
~  и
и  , то
, то 
Свойство 4 особенно важно на практике, т.к. оно фактически означает, что предел отношения бесконечно малых не меняется при замене их на эквивалентные бесконечно малые. Этот факт дает возможность при нахождении пределов заменять бесконечно малые на эквивалентные им функции, что может существенно упростить вычисление пределов.
Пример 22. Найти предел 
Так как  ~
~  и
и 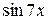 ~
~ 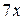 при
при  , то, заменив функции эквивалентными бесконечно малыми, получим:
, то, заменив функции эквивалентными бесконечно малыми, получим: 
Пример 23. Найти предел  .
.
Так как 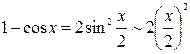 при
при  , то
, то  .
.
Пример 24. Найти предел 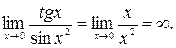
Если  - бесконечно малые при
- бесконечно малые при  , причем
, причем 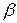 - бесконечно малая более высокого порядка, чем
- бесконечно малая более высокого порядка, чем  , то
, то  - бесконечно малая, эквивалентная
- бесконечно малая, эквивалентная  . Это можно доказать следующим равенством
. Это можно доказать следующим равенством 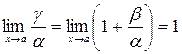 .
.
Тогда говорят, что  - главная часть бесконечно малой функции
- главная часть бесконечно малой функции  .
.
|
|
|
Пример 25. Функция 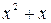 – бесконечно малая при
– бесконечно малая при  ,
, 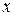 – главная часть этой функции. Чтобы показать это, запишем
– главная часть этой функции. Чтобы показать это, запишем 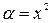 ,
,  , тогда
, тогда  .
.
1.4. Односторонние пределы. Асимптоты.
Если 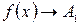 при
при  только при
только при  , то
, то  - называется пределом функции
- называется пределом функции 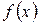 в точке
в точке  слева, а если
слева, а если  при
при  только при
только при  , то
, то 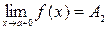 называется пределом функции
называется пределом функции 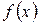 в точке
в точке  справа.
справа.
 у
у
f(x)
А2
А1
0 a x
Приведенное выше определение относится к случаю, когда функция 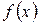 не определена в самой точке
не определена в самой точке  , но определена в некоторой сколь угодно малой окрестности этой точки.
, но определена в некоторой сколь угодно малой окрестности этой точки.
Пределы  и
и  называются также односторонними пределами функции
называются также односторонними пределами функции 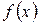 в точке
в точке  . Также говорят, что
. Также говорят, что  – конечный предел функции
– конечный предел функции 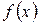 .
.
Односторонние бесконечные пределы и пределы на бесконечности применяются при нахождении асимптот графиков функций.
Будем различать вертикальные и наклонные асимптоты.
Прямая 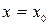 называется вертикальной асимптотой, если справедливо одно из четырех равенств:
называется вертикальной асимптотой, если справедливо одно из четырех равенств:
 (1)
(1)
При построении графиков функций полезно представлять, как изображаются данные пределы. Из существования пределов (1) следует, что при  график функции приближается к вертикальной прямой
график функции приближается к вертикальной прямой 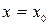 . Схематично изобразим все четыре предела.
. Схематично изобразим все четыре предела.
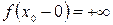



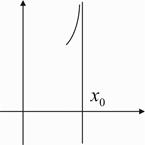
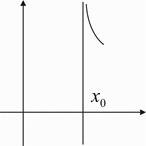
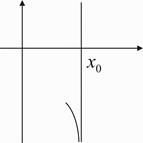
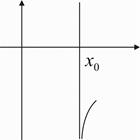
Пример 26.  Прямая
Прямая  является вертикальной асимптотой, так как
является вертикальной асимптотой, так как  . Заметим, что
. Заметим, что 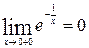 .
.
Прямая  называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 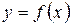 при
при 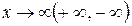 , если
, если 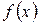 определена на множестве
определена на множестве  , где
, где 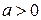 , и
, и
 (2), где
(2), где 
Геометрически это определение означает, что при 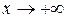 и
и  (или
(или 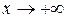 или
или  ) график функции
) график функции 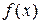 приближается к прямой
приближается к прямой  .
.
Теорема 1. Прямая  называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 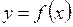 при
при  тогда и только тогда, когда существуют два предела:
тогда и только тогда, когда существуют два предела: 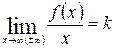 (3);
(3); 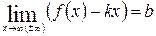 (4)
(4)
Доказательство.
( Необходимость).
Пусть прямая  является наклонной асимптотой графика функции
является наклонной асимптотой графика функции 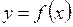 при
при 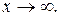 Разделим (2) на
Разделим (2) на 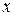 :
: 
Следовательно,
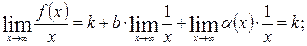
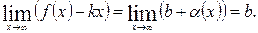
(Достаточность).
Пусть выполнены равенства (3), (4). Обозначим  Из (4) следует, что
Из (4) следует, что 
В частном случае при  наклонная асимптота является горизонтальной.
наклонная асимптота является горизонтальной.
Пример 27. Прямая 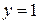 является горизонтальной асимптотой графика функции
является горизонтальной асимптотой графика функции  , поскольку
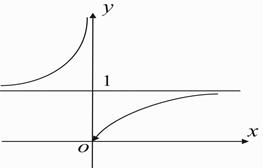
, поскольку 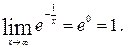 Учитывая (1), схематично построим график функции
Учитывая (1), схематично построим график функции 
 2015-05-30
2015-05-30 10487
10487
