Школьного курса информатики”.
Лабораторная работа 1.
Динамические одномерные и двумерные массивы.
B. Задачи второго, среднего уровня
1. На плоскости задано N точек своими координатами. Найти среди них такую, сумма расстояний от которой до остальных минимальна.
2. В множестве точек на плоскости найти все пары точек с одинаковым максимальным расстоянием между ними.
3. Найти расстояние между двумя заданными множествами точек на плоскости, то есть расстояние между наиболее близко расположенными точками этих множеств.
4. Найти площадь многоугольника, заданного перечислением координат вершин в порядке обхода его границы.
5. Среди заданного множества точек в трёхмерном пространстве M найти такую точку, что шар заданного радиуса с центром в этой точке содержит максимальное количество точек из M.
6. В заданном множестве точек на плоскости выбрать такие три различные точки, чтобы была минимальной разность между количествами точек, лежащих внутри и вне треугольника с вершинами в выбранных точках.
7. Выбрать три точки заданного на плоскости множества точек, составляющие треугольник наибольшего периметра.
8. Многоугольник задан координатами своих вершин. Определите, является ли данный многоугольник выпуклым.
9. Многоугольник задан координатами своих вершин. Найдите площадь этого многоугольника.
10. Заданные точки плоскости рассортировать по возрастанию расстояния от начала координат. Для сортировки использовать алгоритм выбора минимального элемента.
11. Найти значение многочлена с заданными в виде массива коэффициентами, вычисляя и суммируя значения одночленов.
12. Найти значение многочлена с заданными в виде массива коэффициентами, используя схему Горнера.
13. Сложить два многочлена заданных различных степеней, если коэффициенты хранятся в массивах. Все три полинома вывести на экран в удобном для просмотра виде (коэффициенты, равные 1 или –1, не выводить; не выводить одночлен с нулевым коэффициентом и т. п.).
14. В одномерном массиве найти количество различных элементов.
15. Известно, что в массиве размерности N могут быть только целые числа из диапазона 1..31. Рассортировать эти числа по частоте встречаемости, используя алгоритм обмена.
16. Сложить два больших целых числа по правилу сложения “в столбик”. Для таких чисел вещественный тип неприемлем, а типа long
int недостаточно, так как в числе больше 10 цифр. Для хранения такого числа предлагается использовать одномерный массив, каждый элемент которого представляет собой одну десятичную цифру числа.
17. Найти максимальное из чисел, встречающихся в матрице более одного раза.
18. Седловой точкой матрицы назовём такой элемент, который является одновременно максимальным в столбце и минимальным в строке. Найти одну, любую седловую точку заданной матрицы.
19. Для заданной квадратной матрицы найти такие k, что к -я строка совпадает с к -м столбцом.
20. Найти максимальный среди всех элементов тех строк заданной матрицы, которые упорядочены (либо по возрастанию, либо по убыванию).
21. Элемент матрицы называется локальным минимумом, если он строго меньше всех имеющихся у него соседей. Найти количество локальных минимумов заданной матрицы.
22. Выполнить операцию сглаживания для заданной матрицы, в результате которой получается новая матрица того же размера, каждый элемент которой вычисляется как среднеарифметическое имеющихся соседей соответствующего элемента исходной матрицы.
23. Если в заданной матрице нет нулей, то заменить повторяющиеся элементы матрицы нулями и найти количество ненулевых, то есть неповторяющихся элементов. В противном случае матрицу оставить без изменения. Память для новой матрицы не резервировать.
24. Расстояние между k -й и m -й строками матрицы a определяется как 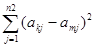 , где n2 — количество элементов в строке матрицы. Указать номер строки, максимально удаленной от первой строки заданной матрицы.
, где n2 — количество элементов в строке матрицы. Указать номер строки, максимально удаленной от первой строки заданной матрицы.
25. Найти строку заданной матрицы, в которой длина максимальной серии упорядоченных по возрастанию элементов минимальна.
26. Взаимно однозначное отображение элементов матрицы на себя можно задать с помощью двух целочисленных матриц: в первой указываем номер строки, куда переходит данный элемент, а во второй – номер столбца. Построить две матрицы, задающие отражение каждого элемента исходной матрицы на симметричный ему элемент относительно главной диагонали.
27. Изменяя порядок следования строк, рассортировать матрицу по возрастанию первых элементов строк. Элементы каждой строки должны остаться без изменений в том же порядке, в котором были до сортировки. Использовать сортировку выбором.
28. Изменяя порядок следования строк, рассортировать матрицу по возрастанию количества нулей в строках. Элементы каждой строки должны остаться без изменений в том же порядке, в котором были до сортировки. Использовать сортировку выбором.
29. Изменяя порядок следования строк, рассортировать матрицу по возрастанию суммы модулей элементов строк. Элементы каждой строки должны остаться без изменений в том же порядке, в котором были до сортировки. Использовать сортировку обменом (алгоритм “пузырька”).
30. Изменяя порядок следования строк, рассортировать матрицу по возрастанию наименьших элементов строк. Элементы каждой строки должны остаться без изменений в том же порядке, в котором были до сортировки. Использовать сортировку обменом (алгоритм “пузырька”).
31. Получить действительную матрицу B, каждый элемент bij которой равен сумме элементов исходной матрицы, расположенных в закрашенной области, определяемой индексами i, j, на рис. 5.
32. Получить действительную матрицу В, каждый элемент bij которой равен сумме элементов исходной матрицы, расположенных в закрашенной области, определяемой индексами i, j, на рис. 6.
33. Получить действительную матрицу В, каждый элемент bij которой равен сумме элементов исходной матрицы, расположенных в закрашенной области, определяемой индексами i, j, на рис. 7.
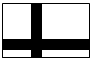 |  | ||||
 | |||||

Рис. 5. Рис. 6. Рис. 7.
 2015-05-30
2015-05-30 1933
1933







