1. На плоскости заданы множество точек P и множество прямых L. Найти две такие различные точки из P, что проходящая через них прямая параллельна наибольшему количеству прямых из L.
2. Среди треугольников с вершинами в заданном множестве точек на плоскости найти такой, стороны которого содержат максимальное количество точек заданного множества.
3. Из заданного множества точек на плоскости выбрать две различные точки так, чтобы разность между количествами точек, лежащих по разные стороны прямой, проходящей через эти две точки, была наименьшей.
4. Задано множество прямых на плоскости (коэффициентами своих уравнений). Найти координаты и количество точек пересечения этих прямых. Если в точке пересекается более двух прямых, такую точку считать как одну.
5. Заданы два множества точек на плоскости. Построить пересечение и разность этих множеств.
6. На плоскости заданы множество точек P и множество окружностей S. Найти две такие различные точки из P, что проходящая через них прямая пересекается с максимальным количеством окружностей из S.
7. На плоскости заданы множество точек P и точка d вне его. Найти количество различных троек точек a, b, c из P таких, что четырёхугольник abcd является параллелограмом.
8. Умножить два полинома заданных различных степеней (не обязательно одинаковых), если коэффициенты хранятся в массивах. Все три полинома вывести на экран в удобном для просмотра виде (коэффициенты, равные 1 или –1, не выводить; не выводить одночлен с нулевым коэффициентом и т. п.).
9. На плоскости задано множество из N точек. Найти такой выпуклый многоугольник, построенный на вершинах из заданного множества, чтобы все точки лежали внутри этого многоугольника. Вывести соответствующее сообщение, если такой многоугольник построить невозможно.
10. На плоскости задано множество точек. Выделить из этих точек вершины квадрата, на сторонах которого лежит наибольшее количество заданных точек.
11. Все элементы целочисленного массива, представляющие собой совершенные числа (равные сумме своих делителей), переписать в начало массива, сохраняя их порядок, а остальные элементы — в конец. Новый массив не формировать.
12. Изменить заданный одномерный массив, чтобы в начале стояли все нулевые элементы, затем – отрицательные, а в конце – положительные элементы последовательности. При этом начальный порядок отрицательных (аналогично и положительных) элементов должен быть сохранён. Новый массив не формировать.
13. Из двух заданных упорядоченных числовых массивов размерности n и m получить новый упорядоченный массив размерности n+m, не используя алгоритма сортировки.
14. В одномерном массиве найти k -й максимальный элемент. Предусмотреть случай, когда такого элемента не существует.
15. Умножить два больших целых числа по правилу умножения “в столбик”. Для таких чисел вещественный тип неприемлем, а типа long
int недостаточно, так как в числе больше 10 цифр. Для хранения такого числа предлагается использовать одномерный массив, каждый элемент которого представляет собой одну десятичную цифру числа.
16. Для заданной квадратной целочисленной матрицы найти максимум среди сумм элементов диагоналей, параллельных главной диагонали матрицы.
17. Для заданной квадратной целочисленной матрицы найти максимум среди сумм элементов диагоналей, параллельных побочной диагонали.
18. Две строки целочисленной матрицы назовём похожими, если совпадают множества чисел, встречающихся в этих строках. Найти количество строк в максимальном множестве попарно непохожих строк заданной матрицы, расположенных подряд.
19. Изменяя порядок следования строк, рассортировать целочисленную матрицу по возрастанию количества симметричных чисел в строке. Элементы каждой строки должны остаться без изменений в том же порядке, в котором были до сортировки. Использовать сортировку вставками.
20. Изменяя порядок следования строк, рассортировать целочисленную матрицу по возрастанию максимальной длины серии упорядоченных по возрастанию элементов строки. Элементы каждой строки должны остаться без изменений в том же порядке, в котором были до сортировки. Использовать сортировку слиянием.
21. По матрице A построить матрицу B того же размера, где элемент bij определяется следующим образом. Через aij проведем в A линии, параллельные сторонам прямоугольника до пересечения с побочной диагональю; bij определяется как максимум среди элементов треугольника в А (рис. 8).
22. По матрице А построить матрицу В того же размера, где bij определяется следующим образом. Через aij проведем в A диагонали, параллельные главной и побочной диагоналям; bij определяется как максимум в закрашенной части матрицы А (рис. 9).
 | |||||||
 |  | ||||||
 | |||||||

Рис. 8. Рис. 9.
23. Найти сумму элементов, расположенных в закрашенной части квадратной матрицы на рис. 10.
24. Найти произведение ненулевых элементов, расположенных в закрашенной части квадратной матрицы на рис. 11.
 |
Рис. 10. Рис. 11.
25. Начиная с центра, обойти по спирали по часовой стрелке все элементы квадратной матрицы, распечатывая их в порядке обхода.
26. Начиная с центра, обойти по спирали против часовой стрелки все элементы квадратной матрицы, распечатывая их в порядке обхода.
27. Заполнить квадратную матрицу размерности n*n по спирали по часовой стрелке числами 1, 2, 3, …,n*n, начиная с элемента, находящегося в верхнем левом углу.
28. Получить квадратную матрицу порядка n, элементами которой являются заданные действительные числа а 1,..., аnn, расположенные в ней по схеме, которая приведена на рис. 12.
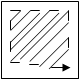 |
Рис. 12.
Лабораторная работа 2 .
Работа со строками и динамическими массивами строк.
 2015-05-30
2015-05-30 2064
2064








