 Пример 1. По проводу, согнутому в виде квадрата со стороной
Пример 1. По проводу, согнутому в виде квадрата со стороной 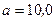 см, течет ток силой
см, течет ток силой 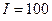 А. Найти магнитную индукцию
А. Найти магнитную индукцию 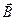 в точке О пересечения диагоналей квадрата.
в точке О пересечения диагоналей квадрата.
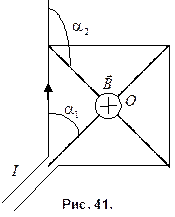
Решение. Сделаем рисунок (рис. 41). Расположим квадратный виток в плоскости чертежа. В точке О определим с помощью правила правого буравчика (векторного произведения) направления 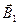 ,
, 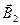 ,
, 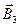 и
и 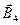 , создаваемые токами, протекающими по каждой стороне квадрата.
, создаваемые токами, протекающими по каждой стороне квадрата.
1. Согласно принципа суперпозиции полей, результирующее поле в точке О
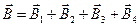 .
.
В точке О все векторы индукции направлены перпендикулярно плоскости витка («от нас»).
Из симметрии следует, что модули этих векторов одинаковы 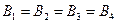 . Следовательно,
. Следовательно, 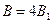 .
.
2. Индукция магнитного поля, создаваемого отрезком прямолинейного провода с током, выражается формулой
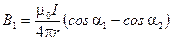 ,
,
где 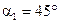 ,
, 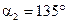 ,
, 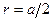 .
.
3. Получим расчетную формулу для первого элемента контура
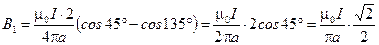 .
.
4. Результирующая индукция в центре квадрата равна
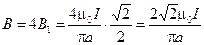 .
.
5. Проведем вычисление
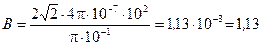 мТл.
мТл.
Ответ: 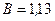 мТл.
мТл.
 Пример 2. С какой силой действует магнитное поле постоянного электрического тока силой
Пример 2. С какой силой действует магнитное поле постоянного электрического тока силой 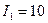 А, текущего по прямолинейному бесконечно длинному проводнику, на контур из провода, изогнутого в виде квадрата? Проводник расположен в плоскости контура параллельно двум его сторонам. Длина стороны контура
А, текущего по прямолинейному бесконечно длинному проводнику, на контур из провода, изогнутого в виде квадрата? Проводник расположен в плоскости контура параллельно двум его сторонам. Длина стороны контура 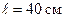 , сила тока в нем
, сила тока в нем 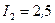 А. Расстояние от прямолинейного тока до ближайшей стороны контура
А. Расстояние от прямолинейного тока до ближайшей стороны контура 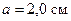 .
.
Решение. Сделаем рисунок (рис. 42). Квадратная рамка с током находится в неоднородном магнитном поле прямого тока. Индукция магнитного поля бесконечного прямого тока
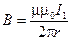 , (1)
, (1)
где r - кратчайшее расстояние от оси проводника до точки, в которой рассчитывается B.
1. Вектор 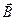 во всех точках рамки направлен перпендикулярно к плоскости рамки. Каждая из сторон рамки - прямолинейный проводник. Поэтому в пределах одной стороны все элементарные силы параллельны друг другу.
во всех точках рамки направлен перпендикулярно к плоскости рамки. Каждая из сторон рамки - прямолинейный проводник. Поэтому в пределах одной стороны все элементарные силы параллельны друг другу.
2. Стороны контура 2 и 4 одинаково расположены по отношению к прямолинейному проводнику, но направления тока в них противоположны, поэтому
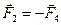 .
.
Результирующая этих сил равна нулю.
3. Стороны контура 1 и 3 параллельны прямому току и находятся от него на расстояниях соответственно 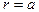 и
и 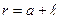 . Силы
. Силы 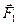 и
и 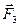 направлены в противоположные стороны. Поэтому результирующая сила
направлены в противоположные стороны. Поэтому результирующая сила
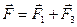 ,
,
ее модуль
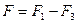 .
.
4. Подставив выражения для r в формулу (1) и учитывая закон Ампера, получим:
для первого элемента контура 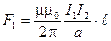 ;
;
для третьего элемента контура 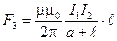 .
.
5. Получим расчетную формулу для результирующей силы действующей на контур
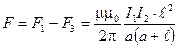 .
.
6. Выполним расчеты
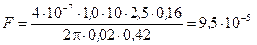 Н.
Н.
Ответ: 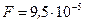 Н.
Н.
 Пример 3. Плоский квадратный контур со стороной
Пример 3. Плоский квадратный контур со стороной 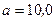 см, по которому течет ток силой
см, по которому течет ток силой 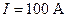 , свободно установился в однородном магнитном поле (
, свободно установился в однородном магнитном поле (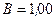 Тл). Определить работу A, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол
Тл). Определить работу A, совершаемую внешними силами при повороте контура относительно оси, проходящей через середину его противоположных сторон, на угол 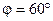 . При повороте контура сила тока в нем поддерживается неизменной.
. При повороте контура сила тока в нем поддерживается неизменной.
Решение. Изобразим контур с током в магнитном поле (рис. 43).
1. На контур с током в магнитном поле действуют силы Ампера, которые в данном случае образуют вращающую пару сил.
2. Вращающий момент пары сил по определению есть произведение плеча на силу и синус угла между ними:
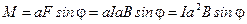 .
.
3. С другой стороны можно записать
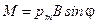 ,
,
где 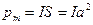 - магнитный момент контура; j - угол между векторами
- магнитный момент контура; j - угол между векторами 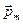 и
и 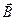 .
.
4. В начальном положении контур свободно установился в магнитном поле. При этом вращающий момент равен нулю 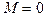 , а, значит,
, а, значит, 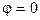 , т.е. векторы
, т.е. векторы 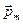 и
и 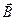 совпадают по направлению. Если внешние силы выводят контур с током из положения равновесия, то возникает момент сил, стремящийся возвратить контур в исходное положение - положение устойчивого равновесия. Против этого момента и будет совершаться работа внешних сил. Так как момент сил переменный (зависит от угла поворота j), то для подсчета работы применим формулу для работы при вращательном движении в дифференциальной форме
совпадают по направлению. Если внешние силы выводят контур с током из положения равновесия, то возникает момент сил, стремящийся возвратить контур в исходное положение - положение устойчивого равновесия. Против этого момента и будет совершаться работа внешних сил. Так как момент сил переменный (зависит от угла поворота j), то для подсчета работы применим формулу для работы при вращательном движении в дифференциальной форме
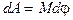 .
.
Подставляя сюда выражение для M, получаем
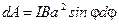 .
.
Возьмем интеграл от этого выражения и найдем работу при повороте контура на любой конечный угол
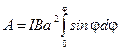 .
.
5. Работа магнитного поля при повороте на угол 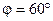
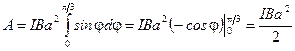 .
.
6. Выразим численные значения в единицах СИ: 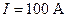 ;
; 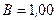 Тл;
Тл; 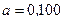 м.
м.
7. Рассчитаем работу
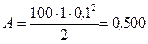 Дж.
Дж.
Ответ: 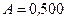 Дж.
Дж.
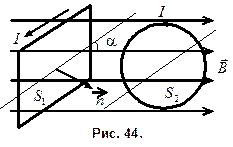 Пример 4. Квадратный контур со стороной
Пример 4. Квадратный контур со стороной 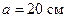 , в котором течет ток 8,0 А, находится в магнитном поле с индукцией 0,50 Тл. Плоскость контура образует с направлением линий индукции угол
, в котором течет ток 8,0 А, находится в магнитном поле с индукцией 0,50 Тл. Плоскость контура образует с направлением линий индукции угол 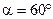 . Какую работу совершат силы Ампера, если при неизменной силе тока в контуре его форму изменить с квадрата на окружность (рис. 44)?
. Какую работу совершат силы Ампера, если при неизменной силе тока в контуре его форму изменить с квадрата на окружность (рис. 44)?
Решение.
1. Работа сил магнитного поля равна
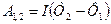 , (1)
, (1)
где 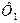 и
и 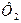 - магнитные потоки сквозь площадь квадрата и окружности. Магнитное поле в пределах контура однородно, а поверхность контура плоская, следовательно
- магнитные потоки сквозь площадь квадрата и окружности. Магнитное поле в пределах контура однородно, а поверхность контура плоская, следовательно
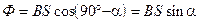 , (2)
, (2)
учитывая это
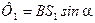 ; (3)
; (3)
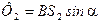 ; (4)
; (4)
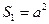 ; (5)
; (5)
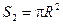 , (6)
, (6)
где R - радиус окружности.
2. Периметры контуров равны: 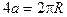 , откуда
, откуда
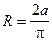 . (7)
. (7)
3. Подставляя (3)-(7) в (1), получаем расчетную формулу:
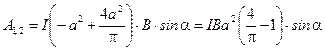 ;
;
4. Выполним расчеты
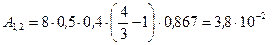 Дж.
Дж.
Ответ: 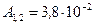 Дж.
Дж.
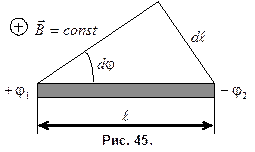 Пример 5. В однородном магнитном поле с индукцией
Пример 5. В однородном магнитном поле с индукцией 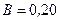 Тл вокруг оси, параллельной линиям индукции, вращается тонкий проводящий стержень длиной
Тл вокруг оси, параллельной линиям индукции, вращается тонкий проводящий стержень длиной 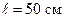 . Ось вращения перпендикулярна к стержню и проходит через один из его концов (рис. 45). Угловая скорость вращения стержня
. Ось вращения перпендикулярна к стержню и проходит через один из его концов (рис. 45). Угловая скорость вращения стержня 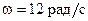 . Найти разность потенциалов между концами стержня.
. Найти разность потенциалов между концами стержня.
Решение. 1. Запишем уравнение электромагнитной индукции Фарадея:
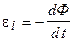 , (1)
, (1)
где dФ - элементарное изменение потока магнитной индукции, сцепленного со стержнем.
2. Разность потенциалов 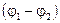 между концами стержня равна по модулю и противоположна по знаку ЭДС индукции
между концами стержня равна по модулю и противоположна по знаку ЭДС индукции 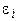 , возникающей в нем при вращении в магнитном поле:
, возникающей в нем при вращении в магнитном поле:
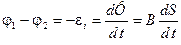 , (2)
, (2)
где B - индукция магнитного поля; dS - площадь, описываемая стержнем за время dt.
3. Найдем элементарную площадь формируемую стержнем при его вращении
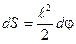 , (3)
, (3)
где 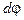 - угол поворота стержня за время dt.
- угол поворота стержня за время dt.
4. Подставляем (3) в (2) и, используя, что 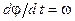 , получаем расчетную формулу
, получаем расчетную формулу
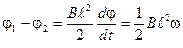 . (4)
. (4)
5. Выполним расчеты искомой величины
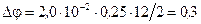 В.
В.
Ответ: 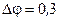 В.
В.
Пример 6. В однородном магнитном поле с индукцией 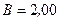 Тл движется протон. Траектория его движения представляет винтовую линию радиуса
Тл движется протон. Траектория его движения представляет винтовую линию радиуса 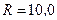 см с шагом
см с шагом 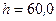 см. Заряд протона равен
см. Заряд протона равен 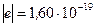 Кл, масса -
Кл, масса - 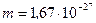 кг. Вычислить кинетическую энергию W протона.
кг. Вычислить кинетическую энергию W протона.
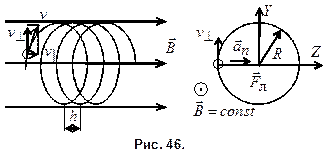 Решение. 1. Составляющая скорости
Решение. 1. Составляющая скорости 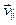 (см. рис. 46) не изменяется ни по модулю, ни по направлению. Составляющая скорости
(см. рис. 46) не изменяется ни по модулю, ни по направлению. Составляющая скорости 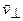 под действием силы Лоренца непрерывно меняет направление, оставаясь постоянной по модулю.
под действием силы Лоренца непрерывно меняет направление, оставаясь постоянной по модулю.
Таким образом, протон участвует в двух движениях: равномерном прямолинейном со скоростью 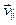 параллельно линиям индукции (вдоль оси OX) и по окружности со скоростью
параллельно линиям индукции (вдоль оси OX) и по окружности со скоростью 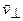 (постоянной по модулю) в плоскости YOZ.
(постоянной по модулю) в плоскости YOZ.
2. Кинетическая энергия протона:
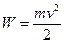 , (1)
, (1)
где
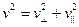 . (2)
. (2)
3. Шаг винтовой линии (смещение вдоль оси OX за время T одного оборота) равен
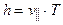 , (3)
, (3)
а период
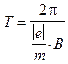 , (4)
, (4)
поэтому
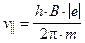 . (5)
. (5)
4. Второй закон Ньютона в случае криволинейного движения имеет вид
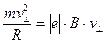 , (6)
, (6)
отсюда найдем перпендикулярную составляющую скорости
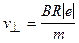 . (7)
. (7)
5. Подставляя выражения (5) и (7) в формулы (1) и (2), получим расчетную формулу для энергии
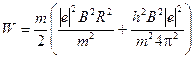 или
или 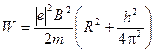 ;
;
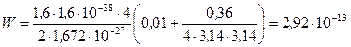 Дж.
Дж.
Ответ: 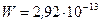 Дж.
Дж.
Пример 7. Соленоид содержит 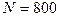 витков. Сечение сердечника из немагнитного материала имеет площадь
витков. Сечение сердечника из немагнитного материала имеет площадь 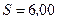 см2. Длина соленоида
см2. Длина соленоида 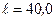 см. По обмотке соленоида протекает ток
см. По обмотке соленоида протекает ток 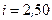 А. Найти среднее значение
А. Найти среднее значение 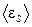 ЭДС самоиндукции, которая возникает в соленоиде, если ток уменьшается практически до нуля за время
ЭДС самоиндукции, которая возникает в соленоиде, если ток уменьшается практически до нуля за время 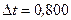 мс.
мс.
Решение.
1. Основной закон электромагнитной индукции:
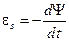 , (1)
, (1)
где Y - потокосцепление контура, определяемое по формуле
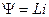 , (2)
, (2)
где L - индуктивность контура.
2. Объединяя (2) и (1), при 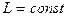 , получаем:
, получаем:
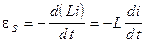 . (3)
. (3)
3. Среднее значение ЭДС самоиндукции
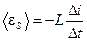 , (4)
, (4)
где 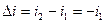 .
.
4. Индуктивность соленоида
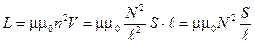 , (5)
, (5)
где n - число витков на единицу длины; магнитная проницаемость среды 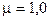 , магнитная постоянная
, магнитная постоянная 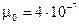 Н/А.
Н/А.
5. Объединив (1)-(4) получим расчетную формулу:
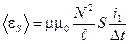 ; (6)
; (6)
6. Произведем расчеты
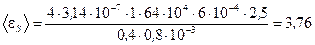 В.
В.
Ответ: 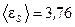 В.
В.
Пример 8. Найти энергию W магнитного поля катушки длиной 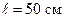 , состоящей из
, состоящей из 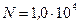 витков, вплотную прилегающих друг к другу (стержень изготовлен из немагнитного материала). Диаметр катушки
витков, вплотную прилегающих друг к другу (стержень изготовлен из немагнитного материала). Диаметр катушки 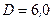 см, а сила тока
см, а сила тока 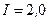 мА.
мА.
Решение.
1. Энергия магнитного поля соленоида с индуктивностью L, по обмотке которого течет ток силой I, выражается формулой
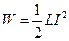 . (1)
. (1)
2. Индуктивность соленоида в случае немагнитного сердечника зависит только от числа витков на единицу длины и от объема сердечника
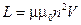 . (2)
. (2)
Учитывая, что 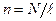 ,
,
 , (3)
, (3)
имеем
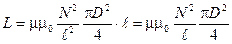 . (4)
. (4)
3. Подставляя (4) в (1), получаем расчетную формулу
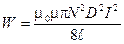 ;
;
4. Выполним расчеты
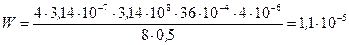 Дж.
Дж.
Ответ: 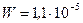 Дж
Дж
 2015-05-30
2015-05-30 21867
21867
